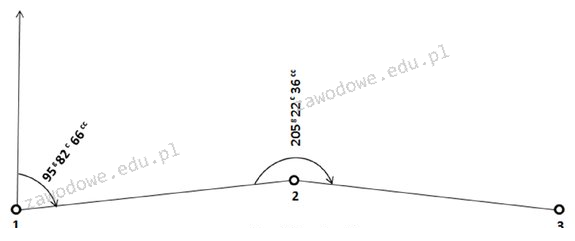
Azymut A2-3 wynoszący 101,0502g jest poprawny, ponieważ obliczenia oparte na zasadach geometrii i pomiarów geodezyjnych zapewniają jego precyzyjność. W geodezji, azymut oznacza kąt pomiędzy kierunkiem północnym a danym kierunkiem, mierzony w kierunku zgodnym z ruchem wskazówek zegara. W tym przypadku, obliczenie azymutu polega na sumowaniu kątów oraz normalizacji wyniku do zakresu od 0g do 400g, co jest standardową praktyką. Przy obliczeniach azymutu ważne jest uwzględnienie błędów pomiarowych, takich jak błędy systematyczne i przypadkowe. Używając odpowiednich narzędzi, takich jak teodolity oraz GPS, można uzyskać wiarygodne wyniki, które są kluczowe w pracach geodezyjnych. Zrozumienie i umiejętność obliczania azymutu jest istotna w różnych dziedzinach, takich jak inżynieria, budownictwo czy nawigacja, co potwierdza jego znaczenie w praktycznych zastosowaniach geodezyjnych.
Zrozumienie azymutu A2-3 i sposobu jego obliczania ma kluczowe znaczenie w geodezji. W przypadku podanych odpowiedzi, widać, że wiele z nich wprowadza w błąd. Na przykład, odpowiedzi takie jak A2-3 = 90,6030g oraz A2-3 = 301,0502g sugerują wartości, które nie są uzasadnione w kontekście norm geodezyjnych. Azymut powinien być mierzony w przedziale od 0g do 400g, a jakiekolwiek wartości wykraczające poza ten zakres wskazują na błędy w obliczeniach lub interpretacji danych. Często zdarza się, że osoby dokonujące obliczeń mylą się, nie uwzględniając kierunku pomiaru czy sumowania kątów. Odpowiedzi takie jak A2-3 = 101,0502g mogą być mylone z innymi wartościami przez nieuwagę lub brak znajomości zasad geometrii. Typowe błędy myślowe obejmują przyjmowanie błędnych założeń dotyczących kierunków lub kątów, co prowadzi do wyciągania niewłaściwych wniosków. Dlatego kluczowe jest, aby przy obliczeniach azymutu zawsze odnosić się do zasad pomiarowych, które wymagają precyzyjnego uwzględnienia wszystkich kątów oraz ich odpowiedniej normalizacji. Przykładem może być sytuacja, w której pomiar kątów nie został przeprowadzony w sposób systematyczny, co może skutkować znacznymi różnicami w uzyskanych wynikach. Z tego powodu, zrozumienie procedur obliczeniowych oraz ich zastosowania w praktyce jest niezbędne dla uzyskania wiarygodnych pomiarów.