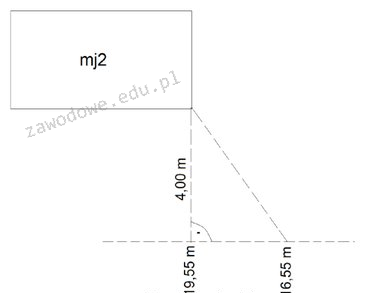
Poprawna odpowiedź to 5,00 m, co odpowiada wartości podpórki wskazanej w zamieszczonym szkicu. W kontekście pomiaru sytuacyjnego szczegółów terenowych metodą ortogonalną, kluczowe jest zrozumienie, że podpórka jest odległością mierzona na prostokątnych osiach układu współrzędnych. Przy wykorzystaniu tej metody, dokładność pomiaru jest kluczowa, a błędy mogą prowadzić do znacznych różnic w dalszych obliczeniach i analizach. W praktyce architektonicznej oraz inżynieryjnej, zastosowanie dokładnych pomiarów terenowych jest niezbędne do tworzenia rzetelnych projektów. Dobre praktyki w tej dziedzinie zalecają stosowanie sprzętu pomiarowego wysokiej precyzji, a także regularne kalibracje urządzeń. Użycie metody ortogonalnej pozwala na uzyskanie nie tylko dokładnych danych o odległościach, ale także o przestrzennym układzie obiektów w terenie, co jest niezwykle istotne w planowaniu inwestycji budowlanych oraz infrastrukturze. Warto zaznaczyć, że w kontekście standardów pomiarowych, dokładność do 5,00 m jest często akceptowana jako minimalny wymóg w wielu branżach, w tym w geodezji, co potwierdza znaczenie tej odpowiedzi.
Wszystkie niepoprawne odpowiedzi wskazują na różne błędy w zrozumieniu pomiarów terenowych oraz zastosowania metody ortogonalnej. Na przykład, podanie odległości 4,00 m może wynikać z nieprawidłowego zrozumienia koncepcji pomiaru w odniesieniu do wymiarowania rzeczywistego obiektu w terenie. Często mylona jest odległość podstawowa z rzeczywistą długością podpórki, co skutkuje błędnymi wynikami. Natomiast odpowiedź 3,00 m może sugerować zbyt dużą pewność w pomiarach, które nie uwzględniają wszystkich istotnych czynników, takich jak zakłócenia terenowe czy błąd sprzętu. Z kolei 6,00 m wskazuje na poważne przeoczenie w analizie, gdzie pomiar rzeczywisty został błędnie oszacowany, co może prowadzić do konsekwencji w dalszych fazach projektowania, zwłaszcza w przypadku dużych inwestycji budowlanych. Podstawowym błędem myślowym w tych odpowiedziach jest niezdolność do uwzględnienia kontekstu pomiarowego oraz specyfiki metody ortogonalnej, która wymaga nie tylko znajomości technik pomiarowych, ale także umiejętności interpretacji wyników w odniesieniu do rzeczywistego układu przestrzennego. Dla poprawnego pomiaru, istotne jest również uwzględnienie standardów branżowych oraz dobrych praktyk w geodezji, co może zapobiec wprowadzeniu błędnych danych do systemów projektowych.