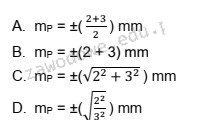Poprawna odpowiedź to "C", ponieważ błąd średni położenia punktu P oblicza się za pomocą wzoru: m<sub>P</sub> = √(m<sub>x</sub><sup>2</sup> + m<sub>y</sub><sup>2</sup>). W przypadku danych, które mamy, m<sub>x</sub> wynosi ±2 mm, a m<sub>y</sub> wynosi ±3 mm. W związku z tym obliczenia wyglądają następująco: m<sub>P</sub> = √(2<sup>2</sup> + 3<sup>2</sup>) = √(4 + 9) = √13 mm. Ta metoda jest zgodna z dobrymi praktykami w geodezji oraz pomiarach, gdzie błąd położenia jest kluczowym parametrem w ocenie dokładności pomiarów. W praktyce, poprawne obliczenie błędu średniego ma istotne znaczenie w kontekście tworzenia map, planowania budynków oraz w inżynierii, gdzie precyzyjne określenie lokalizacji jest niezbędne. Ponadto, standard ISO 17123-1 dotyczący pomiarów geodezyjnych również wskazuje na zastosowanie takich obliczeń w celu zapewnienia jakości i dokładności danych.
W przypadku niewłaściwego podejścia do obliczenia błędu średniego położenia punktu P, często występującym błędem jest brak zrozumienia, że błąd położenia nie jest równy prostemu sumowaniu błędów średnich współrzędnych. Na przykład, niektóre osoby mogą omyłkowo próbować obliczyć m<sub>P</sub> na podstawie średnich wartości błędów, co prowadzi do niepoprawnych wyników. Rzeczywiste błędy w układzie współrzędnych należy brać pod uwagę w postaci ich wartości kwadratowych, a następnie sumować je, aby uzyskać całkowity błąd. Konsekwencją braku zastosowania odpowiednich wzorów jest zaniżenie lub zawyżenie rzeczywistego błędu, co ma bezpośredni wpływ na jakość i dokładność wykonanych pomiarów. Świadomość tego typu błędów jest kluczowa dla profesjonalistów w dziedzinie geodezji, ponieważ niewłaściwe oszacowanie błędów może prowadzić do poważnych konsekwencji w projektach budowlanych czy inżynieryjnych. Dlatego ważne jest, aby w procesie nauki i praktyki stosować odpowiednie metody obliczeniowe, zgodne z normami branżowymi, takimi jak standardy ISO, które wskazują na konieczność stosowania matematycznych podstaw w ocenie błędów pomiarowych.