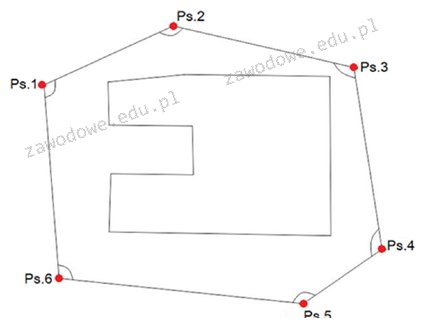
Poprawną odpowiedzią jest 800,0000g, co wynika z zastosowania wzoru na sumę kątów wewnętrznych w wielokącie. Wzór ten to (n-2) * 200g, gdzie n oznacza liczbę boków wielokąta. W przypadku sześciokąta, n wynosi 6, więc obliczenia przedstawiają się następująco: (6-2) * 200g = 4 * 200g = 800g. Zrozumienie tego wzoru jest kluczowe w kontekście geometrii, a także inżynierii, gdzie często potrzeba obliczenia kątów w różnych konstrukcjach. Na przykład, w architekturze czy projektowaniu budynków, ergonomiczne i stabilne kąty są niezbędne dla zapewnienia bezpieczeństwa oraz funkcjonalności obiektów. Znajomość reguł dotyczących kątów wewnętrznych wspiera również praktyki budowlane, w których istotne jest zapewnienie, aby wszystkie elementy były w odpowiednich proporcjach i kształtach. To z kolei wpływa na jakość i trwałość realizacji projektów budowlanych.
Prawidłowe zrozumienie sumy kątów wewnętrznych w wielokącie jest kluczowe w geometrii. Odpowiedzi, które wskazują na wartości takie jak 1600,0000g, 1000,0000g czy 600,0000g, są wynikiem błędnego zastosowania wzoru lub nieporozumienia w zakresie geometrii wielokątów. Często pojawiające się błędy myślowe mogą wynikać z uproszczeń w interpretacji wzorów matematycznych. Na przykład, myśląc o sześciokącie, niektórzy mogą przyjąć, że suma kątów jest wyższa, wskutek nieprawidłowego dodawania kątów lub błędnego wzoru. W rzeczywistości, suma kątów wewnętrznych jest obliczana poprzez uwzględnienie liczby boków wielokąta, co daje nam jasno określony wynik. Błąd w obliczeniach, jak na przykład przyjęcie zbyt dużej liczby dla n, prowadzi do znaczącego przeszacowania wartości, co w praktyce mogłoby skutkować poważnymi błędami w planowaniu konstrukcji architektonicznych. W rzeczywistych projektach budowlanych znajomość tych zasad jest niezbędna, by uniknąć krytycznych błędów, które wpływają na stabilność i bezpieczeństwo obiektów budowlanych. Dlatego ważne jest, aby stosować się do uznawanych standardów i dobrych praktyk w zakresie obliczeń geometrycznych.