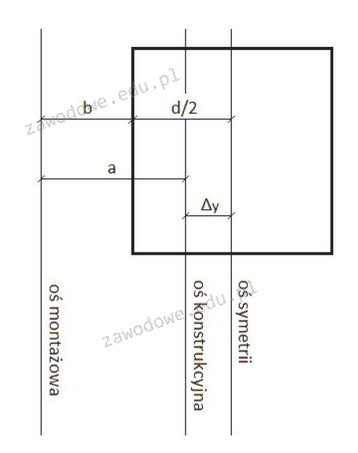
Poprawna odpowiedź, czyli ∆y = (b + d/2) - a, jest wynikiem właściwego zrozumienia zależności geometrycznych w kontekście posadowienia słupa. Wzór ten uwzględnia wszystkie istotne odległości - odległość b od osi montażowej do krawędzi słupa oraz połowę szerokości słupa (d/2), co jest kluczowe dla dokładnego określenia pozycji słupa. Następnie, odejmując od tej sumy odległość a, reprezentującą odległość od osi montażowej do osi konstrukcyjnej, uzyskujemy poziomą odchyłkę ∆y. Tego typu obliczenia są standardem w inżynierii budowlanej, mając na celu zapewnienie, że elementy konstrukcyjne są odpowiednio osadzone i że ich pozycjonowanie spełnia wymogi projektowe. W praktyce, zrozumienie tej zależności jest niezbędne, aby uniknąć problemów związanych z nienależytym posadowieniem, które mogą prowadzić do uszkodzeń konstrukcji w przyszłości. W kontekście norm budowlanych, precyzyjne obliczenia tego typu są kluczowe dla zachowania bezpieczeństwa i trwałości obiektu.
W przypadku nieprawidłowych odpowiedzi, kluczowym błędem jest niewłaściwe zrozumienie relacji pomiędzy odległościami w analizowanym zagadnieniu. Niektóre z proponowanych wzorów, takie jak ∆y = (b - d/2) + a czy ∆y = (d/2 - b) + a, błędnie modyfikują wartości bądź d/2, co prowadzi do nieprawidłowych obliczeń. Przykładowo, w pierwszym przypadku, odejmowanie d/2 z odległości b wprowadza nieścisłości, ponieważ nie uwzględnia pełnej szerokości słupa, co jest kluczowe w kontekście obliczeń związanych z posadowieniem. Z kolei dodawanie wartości a w niektórych wzorach może sugerować, że istnieje jakiś dodatkowy margines do uwzględnienia, co jest mylące, ponieważ wartość a już jest częścią odległości od montażu do konstrukcji. Typowe błędne myślenie może prowadzić do uproszczeń, które nie oddają rzeczywistej geometrii i wymagań projektowych, co w konsekwencji może prowadzić do poważnych błędów w konstrukcji. W praktyce, bardzo ważne jest przestrzeganie standardów branżowych, które precyzyjnie określają, jak należy podejść do tych obliczeń, aby konstrukcje były stabilne i bezpieczne. Zachowanie ostrożności w interpretacji danych wartości jest kluczowe, a zrozumienie praktycznych zastosowań tych wzorów jest niezbędne dla efektywnego projektowania i realizacji budowli.