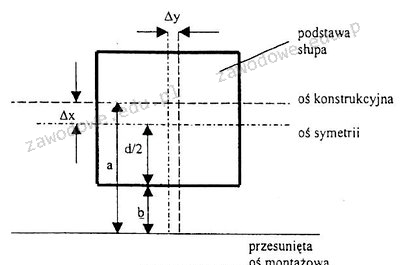
Wzór Δx = a – (d/2 + b) jest właściwy, ponieważ uwzględnia wszystkie istotne odległości w układzie konstrukcyjnym. Odległość a odnosi się do lokalizacji osi konstrukcyjnej, a termin (d/2 + b) opisuje sumę przesunięcia, które składa się z połowy szerokości słupa (d/2) oraz odległości b do przesuniętej osi montażowej. Takie podejście jest zgodne z zaleceniami branżowymi dotyczącymi obliczeń w inżynierii budowlanej, gdzie precyzyjne obliczenia odległości mają kluczowe znaczenie dla stabilności konstrukcji. Poprawne obliczenie poziomej odchyłki jest kluczowe dla zapewnienia, że wszystkie elementy konstrukcji są prawidłowo wyrównane, co przekłada się na ich długoterminową trwałość i bezpieczeństwo. W praktyce, podczas projektowania i wznoszenia obiektów budowlanych, takie obliczenia są często wykorzystywane w celu zmniejszenia ryzyka błędów konstrukcyjnych, co jest szczególnie istotne w projektach o dużym znaczeniu dla bezpieczeństwa publicznego.
Błędne odpowiedzi mają swoje źródło w nieporozumieniach dotyczących geometrii oraz relacji pomiędzy odległościami w kontekście lokalizacji słupa. Odpowiedzi, które sugerują dodanie lub pomijanie odległości b oraz d/2, prowadzą do nieprawidłowych wyniku, ponieważ nie uwzględniają one rzeczywistego położenia osi montażowej w odniesieniu do osi konstrukcyjnej. Niektóre z niepoprawnych wzorów zadają pytania o rolę odległości b i d/2, co może wprowadzać w błąd osoby, które nie zdają sobie sprawy, że sumowanie tych odległości jest kluczowe dla ich poprawnego zrozumienia. Mylne koncepcje mogą wynikać z braku realizacji zasady, że do obliczenia przesunięcia należy uwzględnić zarówno szerokość słupa, jak i odległość do osi montażowej, co jest kluczowe dla stabilności całej konstrukcji. W praktyce, zaniedbanie takich zasad prowadzi do błędów, które mogą mieć poważne konsekwencje w projektach budowlanych, dlatego ważne jest, aby każdy inżynier zrozumiał te relacje i stosował je zgodnie z normami branżowymi.