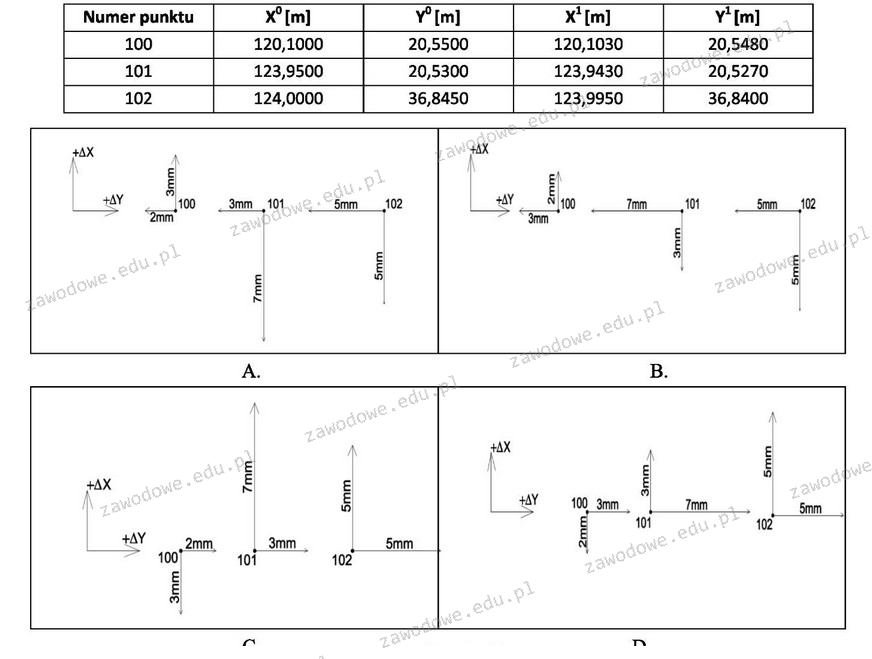
Odpowiedź A jest prawidłowa, ponieważ wektory przemieszczeń punktów 100, 101 i 102 zostały poprawnie przedstawione na rysunku. Analizując dane z tabeli, punkt 100 przemieszcza się o 3 mm w prawo i 2 mm w dół, co jest zgodne z kierunkiem wektora na rysunku A. Punkt 101, który przemieszcza się o 7 mm w lewo i 3 mm w dół, również jest zgodny z opisaną wartością, a jego wektor wskazuje na odpowiednie przesunięcie. Punkt 102, z przemieszczeniem o 5 mm w lewo i 5 mm w dół, znajduje się w spójności z pozostałymi wektorami. W praktyce, przy analizy przemieszczeń konstrukcji, takie przedstawienie wektorów jest niezbędne do oceny ich stabilności oraz bezpieczeństwa. Używając tych danych, inżynierowie mogą podejmować decyzje dotyczące napraw i modyfikacji w budynkach, co jest kluczowe dla zachowania norm budowlanych i standardów bezpieczeństwa.
Wybierając odpowiedź inną niż A, można napotkać typowe pomyłki związane z interpretacją danych z tabeli oraz wizualizacją wektorów przemieszczeń. Kluczowym błędem jest zrozumienie kierunku i wartości przemieszczeń, które są często mylone w kontekście analizy wektorowej. Osoby, które nie dostrzegają różnicy między przemieszczeniem w prawo a w lewo, mogą błędnie zidentyfikować wektory, co prowadzi do fałszywych wniosków. Ponadto, często pojawia się problem z jednostkami miary; w przypadku przemieszczeń budynków, precyzyjne wartości są kluczowe. Wybierając niewłaściwy rysunek, użytkownik może nie dostrzegać, jak ważna jest analiza lokalnych przesunięć w kontekście całej konstrukcji. Dobrym podejściem jest zawsze wizualizacja przemieszczeń na podstawie pomiarów, aby uniknąć takich nieporozumień. W praktyce, zatwierdzanie danych pomiarowych oraz ich wizualizacja powinny być zgodne z przyjętymi standardami inżynieryjnymi, co pozwala na rzetelną ocenę stanu budynku. Dlatego kluczowe jest dokładne zrozumienie, jak interpretować dane z pomiarów oraz ich graficzną reprezentację.