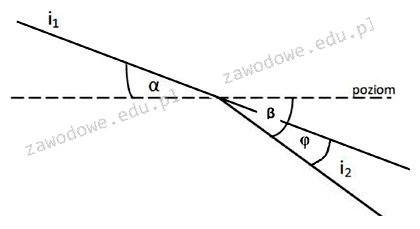
Kąt zwrotu stycznych φ łuku pionowego można wyznaczyć za pomocą wzoru φ = β - α, ponieważ odzwierciedla on różnicę między kątami nachylenia dwóch linii. W praktyce zastosowanie tego wzoru jest niezwykle istotne w wielu dziedzinach inżynierii, takich jak budownictwo czy geodezja. Na przykład, podczas projektowania dróg czy mostów, inżynierowie muszą precyzyjnie określić kąt zwrotu, aby zapewnić odpowiednią widoczność oraz bezpieczeństwo użytkowników. Stosując ten wzór, możemy zrozumieć, jak zmiana jednego z kątów wpływa na całą konstrukcję. Dodatkowo, znajomość geometrii kątów jest niezbędna w kontekście analizy ruchu pojazdów oraz projektowania skrzyżowań, co jest zgodne z najlepszymi praktykami w branży. Również w kontekście kinematyki, zrozumienie tych pojęć pozwala na lepsze modelowanie trajektorii ruchu i przewidywanie interakcji między obiektami w ruchu.
Błędne podejścia do obliczania kąta zwrotu stycznych φ łuku pionowego wynikają z nieprecyzyjnego rozumienia relacji między kątami α i β. Przykładowo, odpowiedź φ = α sugeruje, że kąt zwrotu jest bezpośrednio równy jednemu z kątów nachylenia, co jest niezgodne z zasadami geometrii. W rzeczywistości, kąt zwrotu powinien uwzględniać różnice między tymi kątami, a nie ich bezpośrednią wartość. Z kolei podejście φ = α - β implikuje, że kąt zwrotu jest różnicą w kierunku nachyleń, co również może prowadzić do błędnych interpretacji, szczególnie gdy kąt α jest większy od β. Kąt zwrotu powinien być postrzegany jako miara zmiany kierunku w stosunku do pierwszej linii, a nie jako prosty wynik arytmetyczny. Wreszcie, wzór φ = α + β wprowadza dodatkowy błąd, sugerując, że aby uzyskać kąt zwrotu, należy zsumować oba kąty, co jest sprzeczne z intuicją geometryczną. Takie myślenie prowadzi do nieporozumień, ponieważ zsumowanie kątów nachylenia nie odzwierciedla rzeczywistego zachowania stycznych w kontekście łuku pionowego. Dlatego kluczowe jest, aby nie tylko znać odpowiednią formułę, lecz także rozumieć jej podstawy teoretyczne i praktyczne zastosowania.