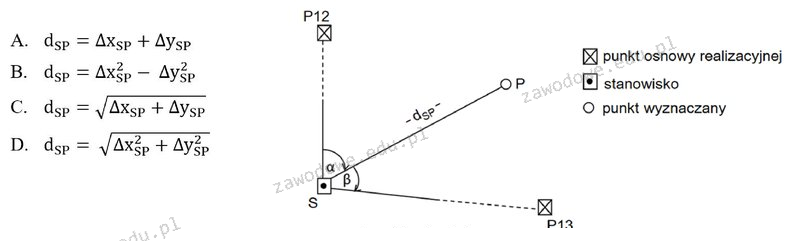
Wybór odpowiedzi D jest poprawny, ponieważ wzór ten opiera się na zasadzie euklidesowej, która jest kluczowa w geometrii analitycznej. Wzór d_{sp} = √(Δx_{sp}² + Δy_{sp}²) jest bezpośrednią aplikacją twierdzenia Pitagorasa, które mówi, że w trójkącie prostokątnym długość przeciwprostokątnej (w naszym przypadku odległość d_{sp}) można obliczyć jako pierwiastek sumy kwadratów długości obu przyprostokątnych (Δx_{sp} oraz Δy_{sp}). Praktyczne zastosowanie tej metody znajduje się w różnych dziedzinach, takich jak inżynieria, architektura, czy geodezja, gdzie precyzyjne ustalanie odległości pomiędzy punktami w przestrzeni jest kluczowe. Ta wiedza przekłada się na standardy pomiarowe, takie jak normy ISO dotyczące geodezyjnych pomiarów, które podkreślają znaczenie stosowania właściwych metod obliczeniowych i pomiarowych, aby zapewnić dokładność i rzetelność danych. Dzięki tej metodzie możemy nie tylko efektywnie określać odległości w terenie, ale także modelować i analizować różne scenariusze przestrzenne.
Wybór innej odpowiedzi niż D sugeruje pewne nieporozumienia dotyczące podstawowych zasad geometrii oraz metod pomiarowych. Niektóre z alternatywnych odpowiedzi mogą odnosić się do bardziej skomplikowanych wzorów lub błędnie interpretować różnice współrzędnych. Kluczową kwestią, którą warto zrozumieć, jest to, że w geometrii analitycznej nie ma innego sposobu na obliczenie odległości euklidesowej w przestrzeni dwuwymiarowej, jak właśnie poprzez zastosowanie wzoru na podstawie twierdzenia Pitagorasa. Inne metody, takie jak stosowanie wzorów trigonometrycznych lub uproszczonych obliczeń, mogą prowadzić do błędnych wyników, ponieważ nie uwzględniają one rzeczywistych różnic w położeniu punktów w układzie współrzędnych. Pojawiające się wątpliwości mogą wynikać z braku zrozumienia, jak różnice w osiach x i y wpływają na całkowitą odległość pomiędzy punktami. W praktyce, nieprawidłowe podejście może prowadzić do błędnych interpretacji danych pomiarowych, co jest nie do przyjęcia w standardach pomiarowych stosowanych w każdym z projektów inżynieryjnych czy architektonicznych. Dobrze jest pamiętać, że w każdym przypadku obliczeń przestrzennych liczy się precyzja i zastosowanie odpowiednich narzędzi matematycznych, aby uniknąć pomyłek.