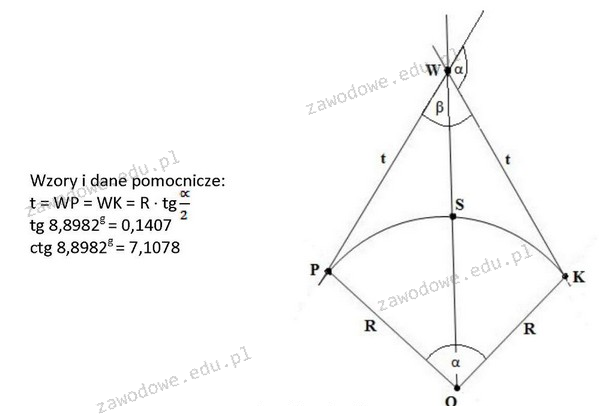
Odpowiedź 59,094 m jest poprawna, ponieważ została obliczona przy użyciu wzoru t = R * tg(α/2), gdzie R to promień łuku, a α to kąt środkowy łuku wyrażony w stopniach. W tym przypadku, promień R wynosi 420,00 m, a kąt α, wynoszący 17°79'63'', po przeliczeniu na stopnie dziesiętne wynosi 17,993° (17 + 79/60 + 63/3600). Następnie obliczamy tangens połowy kąta: tg(α/2) = tg(17,993°/2) = tg(8,9965°). Po obliczeniu tej wartości i pomnożeniu przez promień otrzymujemy długość stycznej głównej t. Takie obliczenia są kluczowe w projektowaniu dróg, gdzie odpowiednie dopasowanie elementów drogi do krzywizn jest niezbędne dla bezpieczeństwa pojazdów. W praktyce inżynieryjnej, znajomość tego typu wzorów i umiejętność ich zastosowania pozwala inżynierom na dokładne projektowanie tras, które są dostosowane do wymagań ruchu drogowego oraz norm dotyczących bezpieczeństwa ruchu.
Wybór niepoprawnej odpowiedzi często wynika z błędnego zrozumienia wzorów i koncepcji związanych z geometrią krzywych. Rozpocznijmy od analizy błędów w podejściu do obliczenia długości stycznej. Bardzo często osoby rozwiązujące tego typu zadania mogą pomylić promień z długością stycznej lub niepoprawnie obliczyć tangens kąta. Niewłaściwe założenie co do jednostek miary, na przykład nieprzekształcenie kątów wyrażonych w stopniach na formę dziesiętną, również prowadzi do błędów w obliczeniach. Ponadto, niektórzy mogą zastosować złą formułę, na przykład zapominając o konieczności podzielenia kąta przez dwa w obliczeniach tangensa. Ważne jest, aby podchodzić do takich problemów systematycznie, upewniając się, że wszystkie jednostki są prawidłowo przeliczone, a wzory zastosowane w sposób właściwy. Kluczowym aspektem jest również zrozumienie znaczenia kąta środkowego w kontekście projektowania dróg. Odpowiednie obliczenie długości stycznej ma bezpośredni wpływ na bezpieczeństwo i komfort jazdy, dlatego znajomość i umiejętność wykorzystania właściwych wzorów i narzędzi jest niezbędna dla każdego inżyniera zajmującego się infrastrukturą drogową.