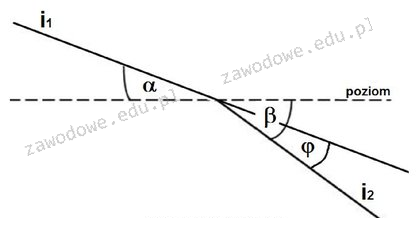
Kąt zwrotu φ, określany jako kąt między dwoma stycznymi do łuku, jest kluczowym pojęciem w geometrii i inżynierii, zwłaszcza w kontekście projektowania dróg i torów. W przypadku kołowego łuku pionowego, kąt zwrotu można obliczyć poprzez różnicę kątów β i α. Kąt β reprezentuje kąt między styczną i2 (w kierunku poziomym) a poziomem, natomiast kąt α to kąt między styczną i1 a poziomem. Zatem, aby uzyskać poprawny kąt zwrotu, musimy odjąć α od β, co prowadzi do wyrażenia φ = β - α. Praktycznie, zrozumienie tego związku jest istotne przy projektowaniu krzywych, aby zapewnić odpowiednią widoczność oraz bezpieczeństwo pojazdów w trakcie manewrów. Analizując te kąty, inżynierowie mogą przewidzieć, jak pojazdy będą się zachowywać na zakrętach, co jest niezbędne do spełnienia norm bezpieczeństwa w projektach infrastrukturalnych.
Wybór niepoprawnej odpowiedzi może być wynikiem niepełnego zrozumienia zależności między kątami α, β i φ. Przyjmowanie, że φ = α, może wydawać się logiczne na pierwszy rzut oka, jednak nie uwzględnia to geometrycznych relacji zachodzących między stycznymi i łukiem. Kąt zwrotu φ nie jest po prostu równy kątowi α, ponieważ α reprezentuje kąt jednej ze stycznych do poziomu, a nie różnicę między dwiema stycznymi. Podobnie, odpowiedź zakładająca, że φ = α + β ignoruje, że suma tych kątów nie oddaje rzeczywistego kątowego rozstawienia stycznych. Z kolei twierdzenie, że φ = α - β, również jest błędne, ponieważ nie uwzględnia faktu, że kąt β jest wyrażeniem większym od kąta α w tym kontekście, co wręcz prowadzi do nieprawidłowych obliczeń. Zrozumienie relacji między tymi kątami jest kluczowe, szczególnie w kontekście inżynieryjnym, gdzie precyzja w obliczeniach kątowych ma bezpośrednie przełożenie na bezpieczeństwo i funkcjonalność projektów. W praktyce, w przypadku projektowania dróg, błędne obliczenie kąta zwrotu może prowadzić do trudności w manewrowaniu pojazdów na zakrętach, co jest niezgodne ze standardami bezpieczeństwa branżowego.