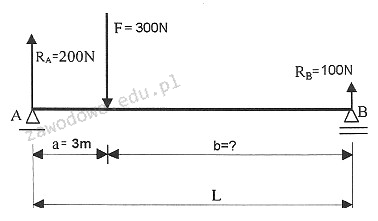
Poprawna odpowiedź to 6 m, ponieważ aby belka pozostała w równowadze, suma momentów sił względem punktu podporowego musi wynosić zero. Moment siły jest obliczany jako iloczyn siły i odległości od punktu obrotu. W praktyce oznacza to, że jeśli mamy na przykład belkę obciążoną na jednym końcu, musimy znaleźć odpowiednią odległość od tego obciążenia do punktu A, aby zrównoważyć momenty. W tym przypadku, gdy zastosujemy zasadę równowagi, otrzymamy, że odległość b wynosi 6 metrów. Przykład zastosowania tej zasady można znaleźć w inżynierii budowlanej, gdzie oblicza się rozmieszczenie ciężarów na dachu czy w konstrukcjach nośnych, aby zapewnić ich stabilność. Zgodnie z zasadami statyki, każda konstrukcja musi być zaprojektowana w taki sposób, aby zachować równowagę pod wpływem różnych sił, co jest kluczowe dla bezpieczeństwa budowli.
W przypadku błędnych odpowiedzi ważne jest zrozumienie, dlaczego obliczenia prowadzące do takich wyników są niewłaściwe. Wiele osób może początkowo sądzić, że zmniejszenie odległości b do 2 m, 9 m lub 1 m sprawi, iż belka pozostanie w równowadze. Jednakże, w rzeczywistości, takie podejścia ignorują podstawowe zasady dotyczące momentów sił. Na przykład, jeżeli przyjmiemy 2 m jako wartość b, moment siły obciążającej belkę nie będzie równy momentowi reakcji w punkcie A, co prowadzi do obrotu belki wokół tego punktu. Podobnie, wartości 9 m i 1 m prowadzą do nieprawidłowego rozkładu sił, co skutkuje niemożnością osiągnięcia stanu równowagi. W kontekście projektów inżynieryjnych, każdy błąd w obliczeniach momentów może mieć poważne konsekwencje, takie jak uszkodzenie konstrukcji lub zagrożenie bezpieczeństwa. Właściwe zrozumienie równowagi momentów jest kluczowe, aby zapobiec takim błędom. Dlatego każdy inżynier powinien być dobrze zaznajomiony z koncepcją równowagi i umieć poprawnie obliczać wartości momentów, co zwykle jest kluczowym elementem w projektowaniu budowli zgodnie z obowiązującymi standardami inżynieryjnymi.