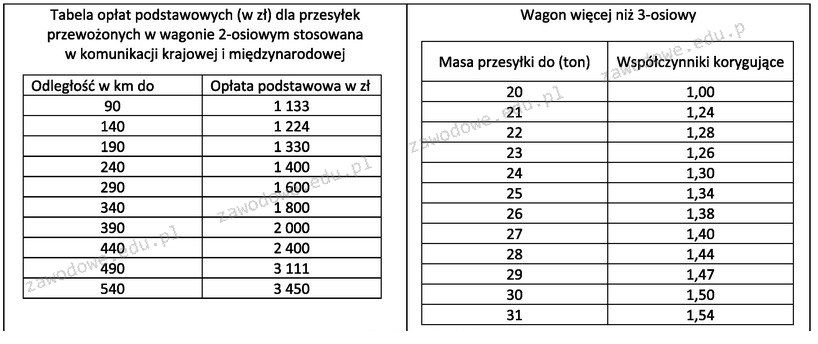
Poprawna odpowiedź to 3 456 zł. Aby obliczyć całkowity koszt przewozu 28 ton ładunku w wagonie czteroosiowym na odległość 423 km, musimy najpierw ustalić opłatę podstawową, która dla tej odległości wynosi 3 111 zł. Następnie, stosując współczynnik korygujący, który dla 28 ton wynosi 1,40, dokonujemy mnożenia: 3 111 zł x 1,40 = 4 355,40 zł. Warto zauważyć, że w praktyce transportu kolejowego stosuje się różne współczynniki korygujące w zależności od tonażu i rodzaju ładunku, co jest istotnym elementem w planowaniu kosztów transportu. Warto również zwrócić uwagę na znaczenie precyzyjnych obliczeń kosztów, które mają kluczowe znaczenie dla efektywności i rentowności operacji transportowych. Przykładem może być analiza kosztów transportu różnych rodzajów ładunków oraz ich wpływ na wybór odpowiednich środków transportu.
Wybór błędnej odpowiedzi może wynikać z nieporozumienia co do zasad obliczania kosztów transportu kolejowego. Należy podkreślić, że każda z podanych wartości, takich jak 2 400 zł, 2 880 zł czy 2 000 zł, jest znacznie zaniżona w stosunku do rzeczywistych kosztów przewozu. Główną przyczyną tego błędu może być nieprawidłowe zrozumienie podstawowych elementów składających się na koszt transportu, takich jak opłata podstawowa oraz współczynniki korygujące. W transporcie kolejowym nie wystarczy znać jedynie odległości; kluczowe jest również uwzględnienie wagi ładunku. Zastosowanie niewłaściwego współczynnika korygującego lub całkowite jego pominięcie prowadzi do błędnych wniosków. Zawężanie analizy przy obliczeniach kosztów transportowych do tylko jednego czynnika, w tym przypadku odległości, jest typowym błędem myślowym, który może zafałszować rzeczywisty obraz kosztów. Dlatego ważne jest, aby przed podjęciem decyzji o wyborze dostawcy usług transportowych zrozumieć, jakie elementy mają wpływ na całkowity koszt przewozu, a także znać standardy i dobre praktyki branżowe w zakresie kalkulacji kosztów transportu.