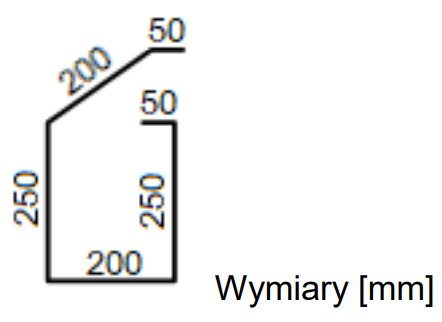
Odpowiedź 0,395 kg jest poprawna, ponieważ opiera się na precyzyjnych danych dotyczących masy jednostkowej pręta stalowego o średnicy 8 mm, która wynosi 0,395 kg/m. Aby obliczyć masę strzemiona, należy najpierw określić całkowitą długość pręta potrzebnego do jego wykonania. W praktyce, znajomość masy jednostkowej materiałów jest istotna w inżynierii i budownictwie, ponieważ pozwala na dokładne obliczenia nie tylko masy, ale również obciążeń, jakie mogą wystąpić w konstrukcjach. Na przykład, w projektach budowlanych, gdzie bezpieczeństwo i stabilność są kluczowe, wykorzystanie prawidłowych danych dotyczących masy materiałów jest niezbędne do skutecznego obliczania nośności elementów. Zrozumienie, jak zastosować te obliczenia w praktyce, jest elementem podstawowym w kształceniu inżynierów. Dodatkowo, w przypadku użycia stali do produkcji elementów konstrukcyjnych, warto zwrócić uwagę na normy i standardy branżowe, które określają wymogi dotyczące jakości materiałów i metod obliczeń.
Wybór niepoprawnej odpowiedzi może wynikać z kilku typowych błędów myślowych, które są powszechne w obliczeniach masy jednostkowej. Często, gdy obliczamy masę elementu, nie uwzględniamy właściwej długości pręta potrzebnego do wykonania strzemiona, co prowadzi do błędnych wyników. Na przykład, jeśli ktoś nie zna długości elementu lub przyjmuje błędne założenia dotyczące wymiarów, może to prowadzić do obliczeń o zaniżonej masie. Inny błąd to nieprawidłowe przemnożenie masy jednostkowej przez długość pręta; czasami osoby podejmujące się obliczeń mylą jednostki lub nie przeliczają ich poprawnie. W odpowiedziach 0,200 kg, 0,222 kg i 0,356 kg można zauważyć, że każde z tych wartości nie ma oparcia w rzeczywistych danych dotyczących masy pręta stalowego o średnicy 8 mm. Aby uniknąć takich pomyłek, kluczowe jest zapoznanie się z tabelami mas jednostkowych oraz ich zastosowaniem w różnych kontekstach inżynieryjnych. Praktyczne umiejętności obliczeniowe są niezwykle istotne, a ich brak może prowadzić do nieprawidłowych wniosków i potencjalnych problemów w projektach budowlanych. Zrozumienie tych błędów jest fundamentalne dla rozwoju umiejętności analitycznych i inżynieryjnych.