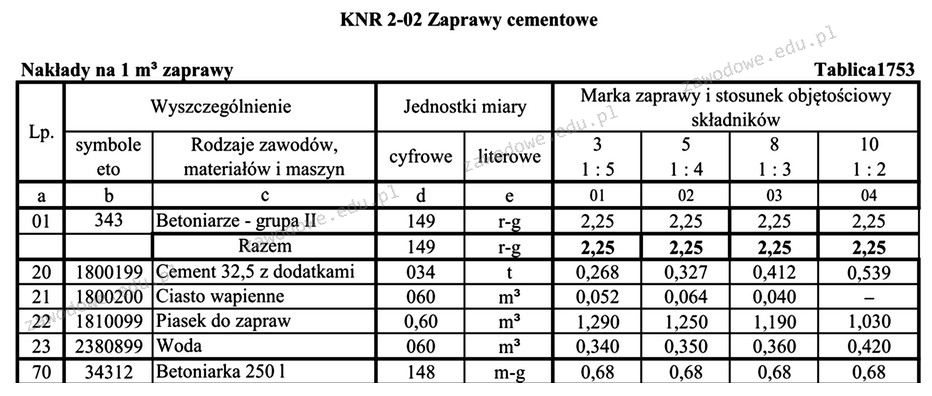
Aby prawidłowo obliczyć ilość cementu potrzebną do wykonania zaprawy cementowej, istotne jest zrozumienie danych zawartych w tabelach KNR (Katalog Norm Rad) oraz przeliczeń jednostkowych. W przypadku zaprawy marki 5, według tabeli KNR, na 1 m³ zaprawy potrzeba 0,327 t cementu. Przekształcając tony na kilogramy, uzyskujemy 327 kg na m³. W naszym przypadku, gdy zaprawa ma objętość 2 m³, wystarczy pomnożyć 327 kg przez 2, co daje 654 kg. Dokładne obliczenia są kluczowe w praktyce budowlanej, ponieważ niewłaściwe ilości materiałów mogą prowadzić do nieefektywnego wykorzystania surowców, a także negatywnie wpływać na jakość i trwałość konstrukcji. Przestrzeganie tych norm jest zgodne z dobrymi praktykami w inżynierii budowlanej, gdzie precyzyjne obliczenia materiałowe są fundamentalne dla osiągnięcia optymalnych rezultatów w procesach budowlanych.
W przypadku błędów w obliczeniach dotyczących ilości cementu potrzebnego do wykonania zaprawy cementowej, warto zwrócić uwagę na kilka kluczowych aspektów związanych z interpretacją danych oraz logiką obliczeń. Często błędne odpowiedzi mogą wynikać z niedokładnego przeliczenia jednostek. Na przykład, jeżeli ktoś pomyli jednostki i zamiast przeliczać tony na kilogramy, pozostanie przy tonach, może dojść do znaczącego niedoszacowania lub przeszacowania potrzebnych materiałów. W przypadku podanych odpowiedzi, niektóre z nich mogą być wynikiem błędnego przeliczenia objętości lub nieprawidłowego zastosowania danych z KNR. Istotne jest również, aby pamiętać, że przy obliczeniach materiałów budowlanych, zawsze należy brać pod uwagę specyfikacje i zbadać normy dotyczące konkretnego rodzaju zaprawy. Użycie niewłaściwych wartości, może prowadzić do problemów z jakością zaprawy, a w efekcie osłabić konstrukcję. Typowe błędy myślowe, które prowadzą do takich pomyłek często obejmują pomijanie kluczowych przeliczników jednostkowych oraz niewłaściwe korzystanie z tabel norm. Dlatego niezwykle ważne jest, aby każdorazowo weryfikować źródła danych oraz ponownie przeliczać wyniki, aby zapewnić prawidłowość obliczeń i bezpieczeństwo w budownictwie.