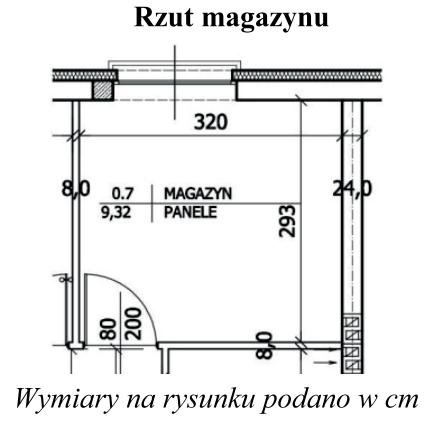
Obliczenie powierzchni ścianki działowej z otworem drzwiowym wymaga uwzględnienia wszystkich istotnych wymiarów pomieszczenia. W tym przypadku wysokość pomieszczenia wynosi 2,75 m. Zastosowanie standardowej formuły do obliczenia powierzchni ścianki działowej oznacza pomnożenie wysokości przez szerokość ścianki. Przyjmując, że szerokość ścianki wynosi 2,64 m, obliczenia dają następujący wynik: 2,75 m (wysokość) * 2,64 m (szerokość) = 7,26 m². Po odjęciu standardowej powierzchni otworu drzwiowego, który wynosi około 0,6 m², otrzymujemy 7,2 m² jako finalny wynik. To podejście jest zgodne z normami budowlanymi oraz dobrymi praktykami w zakresie projektowania i obliczeń inżynieryjnych. Zrozumienie tego procesu jest kluczowe dla prawidłowego planowania przestrzeni oraz budżetowania projektów budowlanych, co stanowi istotny element pracy architekta oraz inżyniera budownictwa.
Przy obliczaniu powierzchni ścianki działowej z otworem drzwiowym, często pojawiają się błędy związane z niepoprawnym uwzględnieniem wymiarów. W niektórych przypadkach uczniowie mogą błędnie przyjmować, że powierzchnia ścianki działowej to po prostu wynik pomnożenia wysokości pomieszczenia przez jego długość, bez uwzględnienia otworów, takich jak drzwi. Przykładowo, odpowiedzi 4,4 m², 6,6 m² oraz 8,8 m² mogą wynikać z niepoprawnych obliczeń, w których nie uwzględniono powierzchni otworu drzwiowego lub z przyjęcia błędnych wymiarów ścianki. Na przykład, odpowiedź 4,4 m² może być wynikiem próby pomnożenia zbyt niskiej wartości wysokości pomieszczenia, co prowadzi do znacznego zaniżenia finalnej wartości. Z kolei odpowiedź 8,8 m² może wynikać z niepoprawnego dodania otworów zamiast ich odjęcia lub z pomyłki przy ustalaniu wymiarów ścianki. Takie błędne podejścia wskazują, że kluczowe jest zrozumienie, jak prawidłowo zastosować formuły do obliczeń powierzchni, aby uwzględnić wszystkie istotne elementy. W kontekście budownictwa, wiedza o prawidłowym wymiarowaniu jest niezbędna, aby uniknąć problemów w realizacji projektów oraz nieporozumień z klientami. Dlatego tak ważne jest przyswojenie sobie zasad obliczeń oraz standardów, które mogą pomóc w uniknięciu takich typowych błędów.