Zgodnie z podaną zasadą oblicz powierzchnię ściany pokazanej na rysunku, jeśli będą tynkowane ościeża otworów.
| Zasada obliczania powierzchni ścian tynkowanych |
| Od powierzchni tynkowanej ściany odlicza się powierzchnię otworów powyżej 3 m2. Od powierzchni tynkowanej ściany nie odlicza się powierzchni otworów do 3 m2, jeśli tynkowane będą ościeża otworu. |
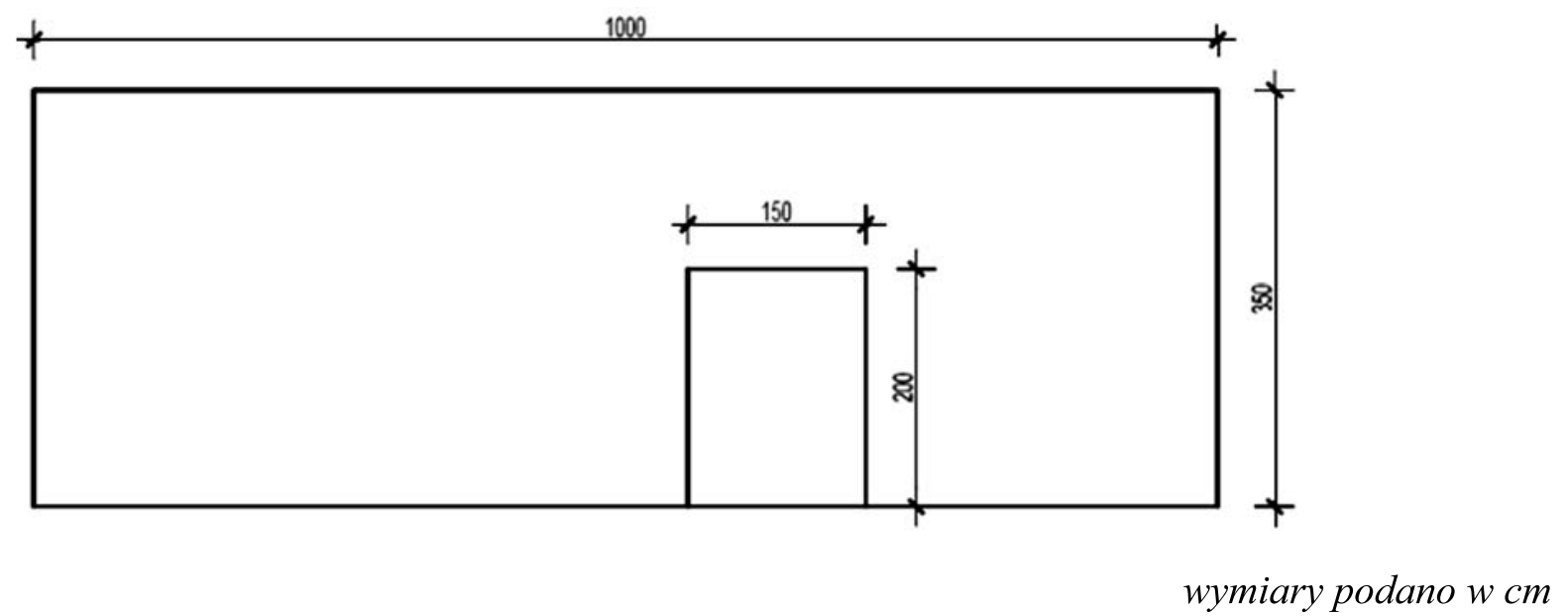
Odpowiedź 35,00 m2 jest na pewno dobra, bo obliczenia dotyczą tynkowania ściany, a tu chodzi o to, jak tynk się stosuje. Cała powierzchnia ściany to 35 m2, a otwór ma 3 m2. Zgodnie z zasadami, jeśli otwór nie przekracza 3 m2, nie odejmujemy go od całej powierzchni, a ościeża też tynkujemy. To jest w porządku i zgodne z tym, co się praktykuje w budownictwie. Gdy planujesz tynkowanie, ważne, żeby patrzeć nie tylko na powierzchnię, ale też na otwory w ścianie, bo to pozwala lepiej wyliczyć, ile materiału i kasy potrzebujesz. Dlatego tynkowanie ościeży, gdy otwór jest niewielki, jest uzasadnione, co potwierdza, że Twoje obliczenia są poprawne.
Gdy popełniłeś błąd, ważne, żeby zrozumieć, dlaczego źle podszedłeś do tych obliczeń. Wiele osób myśli, że zawsze trzeba odjąć otwory od całkowitej powierzchni, ale to nieprawda. To częsty błąd, bo nie do końca rozumie się zasady tynkowania. Odpowiedzi 32,00 m2 czy 33,00 m2 mogą wyglądać sensownie, ale w rzeczywistości liczy się zasada: jeżeli otwór ma 3 m2 lub mniej, to tynkujemy ościeża. Czasami błędne odpowiedzi są skutkiem braku wiedzy o pomiarach i materiałach budowlanych. Ignorowanie tej zasady prowadzi do złych wyników, co może wpłynąć na obliczenia materiałów i cen robót. W budownictwie ważne jest, żeby dobrze rozumieć, jak to wszystko działa, zanim zabierzesz się do liczenia.