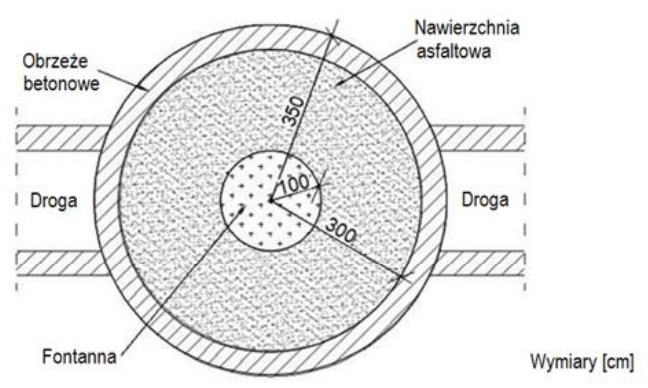
Obliczona powierzchnia nawierzchni asfaltowej wynosząca 25,12 m² jest prawidłowa w wyniku zastosowania właściwych wzorów geometrii do obliczenia powierzchni kół. Aby prawidłowo uzyskać tę wartość, najpierw obliczamy powierzchnię większego koła, które obejmuje jezdnię, a następnie odejmujemy powierzchnię mniejszego koła, które reprezentuje fontannę. Wzór na pole koła to P = π * r², gdzie r to promień koła. W omawianym przypadku promień większego koła wynosi 3,00 m, a mniejszego 1,00 m. Obliczenia prowadzą nas do stwierdzenia, że powierzchnia większego koła to 28,26 m², zaś powierzchnia fontanny to 3,14 m². Odejmując te wartości, uzyskujemy 25,12 m², co jest wartością, na której zostanie ułożona nawierzchnia asfaltowa. Zastosowanie tego rodzaju obliczeń jest kluczowe w inżynierii lądowej i budownictwie, gdzie precyzyjne określenie powierzchni jest istotne dla planowania kosztów i materiałów. Warto również znać standardy dotyczące grubości nawierzchni oraz jej właściwości, co ma wpływ na trwałość i bezpieczeństwo jezdni.
W przypadku błędnych odpowiedzi istotne jest zrozumienie, dlaczego nieprawidłowe obliczenia prowadzą do niewłaściwych wniosków. Wiele osób może błędnie zinterpretować problem, przyjmując za podstawę jedynie dane dotyczące jednego z promieni, co prowadzi do pomyłek w obliczeniach. Na przykład, odpowiadając 35,33 m², można sugerować, że uwzględniono zbyt dużą powierzchnię, nie odliczając właściwie powierzchni fontanny. Z kolei wybór odpowiedzi 28,26 m² może wynikać z obliczenia tylko powierzchni większego koła, co jest błędem koncepcyjnym, ponieważ nie uwzględnia pełnego zakresu zadania. Decydując się na 38,47 m², można błędnie założyć, że zastosowano niewłaściwą wartość promienia lub błędnie obliczono pole, nie respektując konieczności odejmowania. Takie błędy często wynikają z niepełnego zrozumienia wzorów matematycznych oraz ich zastosowania w kontekście praktycznym. Kluczowe jest, aby w procesie nauczania skupiać się na zrozumieniu zasad działania wzorów oraz ich właściwego zastosowania, zamiast na mechanicznej aplikacji formuł. W kontekście inżynieryjnym, umiejętność prawidłowego obliczania powierzchni jest niezbędna, aby uniknąć błędów w projektach budowlanych i związanych z nimi kosztami.