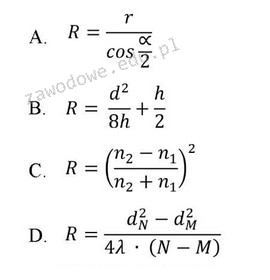Wzór D. jest kluczowy w praktyce optycznej, zwłaszcza w kontekście użycia interferometru do określenia promienia krzywizny soczewki. Jego zastosowanie opiera się na analizie prążków interferencyjnych, które są wynikiem nakładania się fal świetlnych przechodzących przez soczewkę. Poprawna interpretacja różnicy między liczbą prążków N i M, zmierzonych dla dwóch różnych odległości d1 i d2, umożliwia precyzyjne obliczenie promienia krzywizny R soczewki. Taki pomiar jest istotny dla wielu aplikacji, w tym w projektowaniu optyki precyzyjnej oraz w ocenie jakości soczewek w systemach optycznych, gdzie odpowiednia krzywizna ma kluczowe znaczenie dla jakości obrazu. Ponadto, stosowanie tego wzoru wspiera uwzględnienie długości fali λ, co jest zgodne z dobrymi praktykami w pomiarach optycznych. Ostatecznie, znajomość tego wzoru i jego implementacja w praktyce czyni proces pomiaru bardziej efektywnym i dokładnym, co jest niezbędne w zaawansowanych zastosowaniach inżynieryjnych.
Wybór wzoru innego niż D. odzwierciedla powszechny błąd w rozumieniu metod pomiarowych w optyce. Istotne jest zauważenie, że inne wzory mogą nie uwzględniać kluczowych parametrów, takich jak różnica liczby prążków interferencyjnych, co prowadzi do nieprecyzyjnych wyników w wyznaczaniu promienia krzywizny soczewki. W kontekście interferometrii, każdy wzór powinien być oparty na rzeczywistych pomiarach różnic fazowych, które są bezpośrednio powiązane z geometrią soczewki i długością fali światła. Nieodpowiednie podejście do analizy danych interferencyjnych, takie jak pomijanie istotnych wartości odległości d1 i d2, może prowadzić do błędnych wniosków i zafałszowania wyników. W praktyce, niektóre błędne wzory mogą sugerować, że pomiar promienia krzywizny można przeprowadzić bez uwzględnienia interferencji, co jest istotnym nieporozumieniem. Właściwe zrozumienie i zastosowanie wzoru D. jest niezbędne dla uzyskania wiarygodnych wyników, a jego znajomość powinna być fundamentem dla każdego specjalisty w dziedzinie optyki. Dlatego tak ważne jest, aby w procesie nauki i praktyki kłaść nacisk na właściwe metody obliczeniowe i ich zastosowanie w rzeczywistych eksperymentach optycznych.