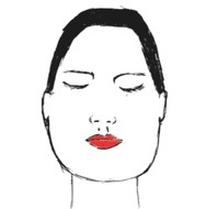
Odpowiedź "trapezoidalnym" jest prawidłowa, ponieważ kształt twarzy na rysunku rzeczywiście przypomina trapez. Charakteryzuje się szerszą górną częścią i zwężającą się dolną częścią, co jest kluczowe dla identyfikacji tego kształtu. W praktyce, rozpoznawanie kształtów twarzy jest istotne w wielu dziedzinach, w tym w kosmetologii, gdzie formułowanie strategii konturowania twarzy opiera się na typach kształtów. W przypadku twarzy trapezoidalnej, odpowiednie techniki makijażu mogą pomóc w optycznym wydłużeniu dolnej partii twarzy i zbalansowaniu jej proporcji. Zrozumienie kształtów twarzy jest również ważne w modzie i stylizacji, gdzie dobór fryzury i okularów powinien być zgodny z kształtem twarzy, aby podkreślić atuty i zniwelować ewentualne niedoskonałości. W branży projektowania, estetyka linii i kształtów odgrywa kluczową rolę w tworzeniu produktów, które są zarówno funkcjonalne, jak i wizualnie atrakcyjne, co powinno być oparte na solidnym zrozumieniu podstawowych zasad geometrii.
Wybór kształtu "romboidalnym" jest błędny, ponieważ romb jest figurą o czterech bokach o jednakowej długości, a kształt twarzy na rysunku nie spełnia tych kryteriów. Charakterystyczne dla rombu są również kąty, które nie są prostokątne, podczas gdy twarz trapezoidalna ma inną strukturę, gdzie górna część jest szersza, a dolna zwęża się. Z kolei odpowiedź "kwadratowym" wskazuje na równą długość wszystkich boków oraz kąty prostokątne, co jest niezgodne z przedstawioną twarzą. Twarz trapezoidalna nie ma równych proporcji, dlatego wybór kwadratu jest również nietrafiony. Odpowiedź "prostokątnym" sugeruje, że twarz ma dwa boki o tej samej długości i dwa inne, co również nie odpowiada kształtowi na rysunku. W kontekście analizy kształtów, kluczowe jest zrozumienie różnic pomiędzy tymi figurami, co jest istotne w wielu zastosowaniach praktycznych, takich jak design, architektura czy stylizacja. Wybierając niewłaściwe odpowiedzi, można dojść do mylnych wniosków o proporcjach i kształcie, co utrudnia dalsze analizy oraz zastosowanie tej wiedzy w praktyce. Użycie precyzyjnych terminów geometrycznych w takich analizach jest kluczem do efektywnego rozumienia i zastosowania teorii w praktycznym życiu.