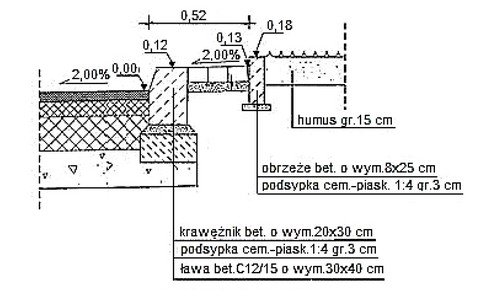
Oblicz objętość ław betonowych o wymiarach jak na zamieszczonym szczególe konstrukcji nawierzchni drogi pod krawężnikami ustawionymi po dwóch stronach jezdni drogi o długości 50 m.
Obliczenie objętości ław betonowych o podanych wymiarach opiera się na fundamentalnych zasadach obliczeń geometrii przestrzennej. Wzór na objętość prostopadłościanu (V = a * b * c) jest kluczowy w tym kontekście, gdzie a i b to wymiary podstawy ławy, a c to jej długość. W naszym przypadku ława ma wymiary 0,30 m na 0,40 m, co daje nam pole podstawy 0,12 m² dla jednego metra długości. Ponieważ ławy są umieszczone po obu stronach drogi, musimy pomnożyć tę wartość przez 2, co daje 0,24 m². Mnożąc przez długość drogi wynoszącą 50 m, otrzymujemy objętość 12,00 m³. To obliczenie jest zgodne z najlepszymi praktykami w zakresie projektowania infrastruktury drogowej, gdzie precyzyjne obliczenia objętości materiałów są kluczowe dla kosztorysowania oraz prawidłowego wykonania robót budowlanych. Codzienna praktyka inżynieryjna wymaga takich obliczeń, aby zapewnić bezpieczeństwo i trwałość konstrukcji.
W przypadku błędnych odpowiedzi na to pytanie, najczęściej spotyka się nieporozumienia związane z podstawowymi zasadami obliczania objętości. W odpowiedziach 0,60 m³ i 6,00 m³ można zauważyć, że błąd polega na niewłaściwym zrozumieniu wymiarów ław betonowych lub sposobu ich obliczania. Często spotykanym błędem jest pomijanie faktu, że ławy betonowe są umieszczone po obu stronach drogi, co powinno być uwzględnione w obliczeniach. Przykładowo, osoby wybierające 0,60 m³ mogą błędnie obliczać objętość jednej ławy zamiast uwzględniać całość. Natomiast wybór 6,00 m³ może wynikać z nieprawidłowego pomnożenia objętości przez długość drogi, bez uwzględnienia dodatkowego wpływu ław znajdujących się po obu stronach. Odpowiedź 120,00 m³ wskazuje na skrajnie zawyżoną wartość, co może świadczyć o całkowitym niezrozumieniu zasady obliczania objętości prostopadłościanu. Kluczowym elementem w takich obliczeniach jest zrozumienie, że objętość całkowita budowli jest wynikiem pomnożenia wymiarów podstawy przez długość, przy prawidłowym uwzględnieniu wszystkich elementów konstrukcyjnych. Analizując te błędy, należy zwrócić uwagę na to, jak ważne jest dokładne zrozumienie wszystkich parametrów w procesach obliczeniowych oraz unikanie uproszczeń, które mogą prowadzić do znaczących różnic w wynikach.