Kwalifikacja: ELM.02 - Montaż oraz instalowanie układów i urządzeń elektronicznych
Zawód: Technik elektronik
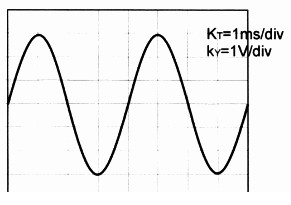
Ile wynosi częstotliwość sygnału przedstawionego na oscylogramie?
Odpowiedzi
Informacja zwrotna
Częstotliwość sygnału, którą obliczyliśmy na podstawie okresu wynoszącego 4 ms, wynosi 250 Hz. To dlatego, że częstotliwość jest odwrotnością okresu, co możemy zapisać matematycznie jako f = 1/T, gdzie f to częstotliwość, a T to okres. W praktyce, znajomość częstotliwości sygnału jest kluczowa w wielu dziedzinach inżynierii, takich jak telekomunikacja, elektronika czy automatyka. Na przykład, w systemach komunikacyjnych, częstotliwość sygnału wpływa na jego zdolność do przesyłania informacji. Standardy takie jak IEEE 802.11, używane w sieciach bezprzewodowych, definiują częstotliwości operacyjne, które muszą być zgodne z regulacjami, aby zapewnić optymalne działanie i minimalizować zakłócenia. Zrozumienie, jak obliczać i interpretować częstotliwości sygnałów, jest kluczowe w projektowaniu złożonych systemów elektronicznych oraz w diagnostyce i konserwacji urządzeń elektronicznych.
Odpowiedzi, które wskazałeś, mogą wydawać się atrakcyjne na pierwszy rzut oka, ale kryją w sobie istotne nieporozumienia dotyczące koncepcji częstotliwości i okresu. Częstotliwość sygnału jest miarą, która mówi nam, ile cykli sygnału występuje w jednostce czasu, a jej obliczenie opiera się na dokładnym pomiarze okresu. Najczęściej, w przypadku okresu wyrażonego w milisekundach, istnieje mylne przekonanie, że częstotliwość może być obliczana w sposób nieodpowiedni, prowadząc do błędnych wyników. Na przykład, jeśli ktoś błędnie interpretuje okres sygnału jako dłuższy niż jest w rzeczywistości, otrzyma znacznie niższą częstotliwość, jaką możemy zobaczyć w odpowiedziach 40 Hz lub 400 Hz. Ponadto, koncepcja 250 kHz może wprowadzać w błąd, wskazując na znacznie wyższą częstotliwość, która nie odpowiada rzeczywistości przedstawionego oscylogramu. Zrozumienie wzajemnych zależności między okresem a częstotliwością jest kluczowe i powinno być podejmowane z należytą starannością. Niezrozumienie tych podstawowych pojęć prowadzi do typowych błędów myślowych, które mogą zafałszować analizę sygnałów oraz ich zastosowanie w praktyce inżynieryjnej.