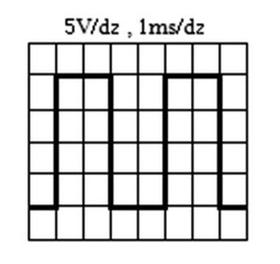
Odpowiedź 250 Hz jest poprawna, ponieważ obliczenia oparte na przedstawionym obrazie oscyloskopu są dokładne. Z analizy wynika, że okres fali prostokątnej T wynosi 4 ms, co odpowiada 4 podziałkom na osi czasowej, gdzie każdy podział to 1 ms. Częstotliwość fali jest określona wzorem f = 1/T, co pozwala na obliczenie f = 1/(4*10^-3 s) = 250 Hz. Zrozumienie częstotliwości fali prostokątnej jest kluczowe w wielu dziedzinach, takich jak elektronika, telekomunikacja oraz przetwarzanie sygnałów. Fale prostokątne są często używane w praktycznych zastosowaniach, takich jak generatory sygnałów, modulacja oraz w obwodach cyfrowych, gdzie sygnały muszą mieć wyraźnie określoną częstotliwość. Ponadto, znajomość częstotliwości sygnałów jest istotna dla inżynierów zajmujących się projektowaniem układów elektronicznych, aby zapewnić kompatybilność i odpowiednią jakość sygnału.
Częstotliwości 5 kHz, 500 Hz oraz 2,5 kHz są błędne, gdyż opierają się na niewłaściwym rozumieniu okresu fali prostokątnej. Często mylone jest pojęcie częstotliwości z pojęciem okresu. Częstotliwość fali to odwrotność okresu, co oznacza, że aby obliczyć częstotliwość, należy znać czas trwania jednego pełnego cyklu fali. W przypadku fali prostokątnej, która trwa 4 ms (co jest równoważne 4 podziałkom na oscyloskopie), obliczenie częstotliwości wymaga zastosowania wzoru f = 1/T. Błędne odpowiedzi mogą wynikać z nawyku pomijania precyzyjnych pomiarów lub z niepoprawnego zrozumienia jednostek miary. Na przykład, 5 kHz wskazuje na bardzo szybkie zmiany sygnału, co nie jest zgodne z zaobserwowanym okresem. Z kolei 500 Hz oraz 2,5 kHz sugerują, że okres fali jest krótki, co również nie odzwierciedla rzeczywistego czasu trwania fali przedstawionego na oscyloskopie. W praktyce, zapamiętanie, że 1 kHz to 1 cykl na milisekundę, może pomóc w uniknięciu tego typu błędów. W związku z tym ważne jest, aby przy analizie sygnałów zwracać uwagę na precyzyjne wartości oraz układy jednostek, co jest kluczowe dla prawidłowego zrozumienia tematu i zastosowania go w realnych aplikacjach.