Kwalifikacja: MEC.03 - Montaż i obsługa maszyn i urządzeń
Zawód: Technik mechanik
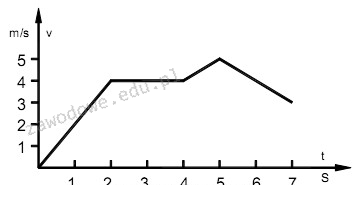
Na wykresie przedstawiono zależność prędkości ciała w funkcji czasu. W którym przedziale prędkość ciała była stała?
Odpowiedzi
Informacja zwrotna
Odpowiedź "2 - 4 s" jest prawidłowa, ponieważ na wykresie prędkość ciała jest stała w tym przedziale czasowym. Linia wykresu jest pozioma, co oznacza, że prędkość nie zmienia się w tym okresie. W praktyce, zrozumienie, kiedy prędkość jest stała, jest kluczowe w wielu dziedzinach, takich jak inżynieria czy fizyka. Na przykład, w analizie ruchu pojazdów, stała prędkość może znacząco wpływać na obliczenia dotyczące czasu przejazdu i zużycia paliwa. W kontekście standardów branżowych, takie analizy są niezbędne w planowaniu tras logistycznych, gdzie prognozowanie czasu dostawy jest kluczowe. Ponadto, stała prędkość jest często wykorzystywana w eksperymentach laboratoryjnych, gdzie precyzyjne pomiary są fundamentalne dla uzyskania dokładnych wyników. Zrozumienie tego konceptu przyczynia się do lepszego modelowania i analizy różnych systemów dynamicznych.
Wybór przedziałów czasowych, w których prędkość nie jest stała, może wynikać z niepełnego zrozumienia, jak interpretować wykresy prędkości. Na przykład, odpowiedzi "4 - 5 s", "1 - 2 s" oraz "5 - 7 s" wskazują na okresy, gdy prędkość ciała zmieniała się, co można zaobserwować dzięki nachyleniu linii na wykresie. W okresach od 1 do 2 sekund oraz od 4 do 5 sekund, linie są nachylone, co wskazuje na zmiany prędkości ciała, co jest klasycznym błędem w analizie wykresów. Często uczniowie mylnie zakładają, że jeśli linia nie jest całkowicie pionowa, to prędkość jest stała, co jest nieprawidłowe. Zmienność prędkości jest istotnym elementem ruchu, i jej właściwe rozumienie jest niezbędne dla analizy różnych zjawisk fizycznych. Aby uniknąć takich błędów, warto zwrócić uwagę na kształt wykresu i jego nachylenie. Przykłady z życia codziennego, takie jak jazda samochodem, ilustrują, jak często prędkość zmienia się niepostrzeżenie, co można zauważyć na wykresach prędkości w różnych sytuacjach. Kluczowe jest, aby na wykresach zachować uwagę na okresy, w których prędkość jest stała, co jest fundamentalnym aspektem analizy ruchu.