Kwalifikacja: BUD.25 - Organizacja, kontrola i sporządzanie kosztorysów robót wykończeniowych w budownictwie
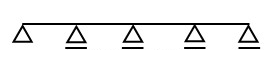
Belka ciągła przedstawiona na rysunku jest statycznie niewyznaczalna
Odpowiedzi
Informacja zwrotna
Belka ciągła jest statycznie niewyznaczalna trzykrotnie, co oznacza, że nie możemy wyznaczyć wszystkich reakcji podporowych jedynie na podstawie klasycznych równań statyki. W analizie belek ciągłych istotne jest zrozumienie, że każda reakcja podporowa, w tym siły pionowe i poziome, wpływa na wewnętrzne stany naprężenia. W omawianym przypadku mamy do czynienia z sześcioma reakcjami podporowymi: cztery są pionowe (od dwóch podpór) i dwie poziome (od dwóch innych podpór). Statyczna równowaga wymaga jedynie trzech równań - sumy sił w kierunku pionowym, sumy sił w kierunku poziomym oraz sumy momentów. Stąd obliczenia wskazują, że liczba reakcji niewyznaczalnych wynosi 3, co wskazuje na statyczną niewyznaczalność belki. Przykładowo, w inżynierii budowlanej, znajomość tego rodzaju analiz jest kluczowa przy projektowaniu elementów nośnych, co przekłada się na bezpieczeństwo konstrukcji oraz jej odpowiednią funkcjonalność.
Wybierając odpowiedź niewłaściwą, można wpaść w pułapkę błędnych założeń dotyczących liczby reakcji podporowych w belkach. Na przykład, wybór liczby jednokrotnej lub dwukrotnej może wynikać z mylnego przeświadczenia, że belka z jedną lub dwiema podporami może być w pełni zbalansowana jedynie przy użyciu minimalnej liczby równań statyki. W rzeczywistości jednak w przypadku belki ciągłej, jej konstrukcja często wymaga analizy więcej niż standardowych dwóch równań równowagi. Z kolei odpowiedź czterokrotna może sugerować nadmiarowe podejście, w którym przyjmuje się, że każda reakcja wymaga osobnego równania, co jest błędne. W kontekście statyki układów, istotne jest, aby poprawnie rozpoznać, ile równań jest dostępnych oraz jakie reakcje można z nich wywnioskować. Typowym błędem, który prowadzi do takich niepoprawnych wniosków, jest niedostateczne zrozumienie zależności między ilością reakcji a ilością dostępnych równań statyki. W praktyce inżynieryjnej, wiedza o statycznej niewyznaczalności jest niezbędna, aby zapewnić odpowiednią stabilność oraz bezpieczeństwo konstrukcji inżynierskich.