Jeżeli pomiary wykonano tak, jak na przedstawionym rysunku, to odległość między punktami osnowy geodezyjnej d1-2 można obliczyć, stosując działanie
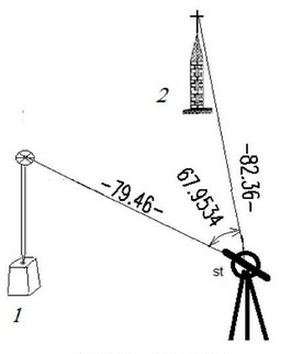
Poprawna odpowiedź opiera się na zastosowaniu twierdzenia cosinusów, które jest kluczowe w geodezji do obliczania długości boków trójkątów. W sytuacji, gdy znamy długości dwóch boków oraz miarę kąta między nimi, możemy z łatwością obliczyć trzeci bok. W przedstawionym przypadku, wzór (d1-2)² = 82,362 + 79,462 - 2 * 82,36 * 79,46 * cos 67,9534g pokazuje, jak wykorzystać te dane do precyzyjnych obliczeń geodezyjnych. W praktyce, takie obliczenia są niezwykle istotne przy tworzeniu map, pomiarach gruntów czy projektach budowlanych, gdzie dokładność jest kluczowa. Przykład użycia tego wzoru można znaleźć w projektach inżynieryjnych, gdzie każdy błąd w pomiarach może prowadzić do poważnych konsekwencji finansowych i czasowych. Warto również zaznaczyć, że znajomość i umiejętność stosowania twierdzenia cosinusów to absolutna podstawa w edukacji geodezyjnej i inżynieryjnej, co podkreśla znaczenie solidnych fundamentów teoretycznych w praktyce.
Wiele z dostępnych odpowiedzi wykazuje braki w zrozumieniu podstawowych zasad geometrii i zastosowania twierdzenia cosinusów. Przykładowo, pierwsza odpowiedź nie odnosi się do geometrycznych relacji między bokami trójkąta ani do kątów, co jest kluczowe w obliczeniach geodezyjnych. Wzór w tej odpowiedzi sugeruje zastosowanie sinusów, co nie jest zgodne z wymaganymi warunkami, gdyż nie mamy do czynienia z funkcją sinusową w kontekście tych pomiarów. Również odpowiedź trzecia odnosi się do zastosowania sinusa w sposób nieprawidłowy, co może wynikać z mylnego zrozumienia relacji w trójkącie. Dodatkowo, odpowiedź czwarta sugeruje użycie tangensa, co jest zupełnie nieadekwatne w przypadku, gdy mamy do czynienia z obliczaniem długości boku, a nie kąta. W geodezji kluczowe jest zrozumienie, że stosowanie niewłaściwych wzorów prowadzi do niedokładnych wyników, które mogą wpływać na cały proces pomiarowy. Te błędy mogą wynikać z braku znajomości właściwych wzorów matematycznych i ich zastosowania w praktyce, co podkreśla znaczenie solidnych podstaw teoretycznych dla każdego geodety czy inżyniera.