Na podstawie danych z rysunku oblicz współrzędne X i Y naroża B realizowanego budynku.
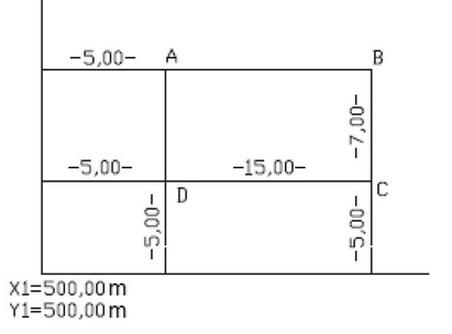
Poprawna odpowiedź dotycząca współrzędnych naroża B (XB = 512,00 m, YB = 520,00 m) jest uzasadniona zgodnie z zasadami geometrii budowlanej. Współrzędne punktu B uzyskujemy poprzez dodanie długości odcinków AB i AD do współrzędnych punktu A, które wynoszą 500,00 m na obu osiach. W tym przypadku, długość odcinka AB wynosi 12,00 m, a odcinka AD 20,00 m. Po obliczeniach: XB = 500,00 m + 12,00 m = 512,00 m oraz YB = 500,00 m + 20,00 m = 520,00 m, co daje prawidłowe współrzędne naroża B. W praktyce, umiejętność dokładnego obliczania współrzędnych punktów w projekcie budowlanym jest kluczowa dla precyzyjnego rozmieszczenia elementów konstrukcyjnych oraz zgodności z planami architektonicznymi. Zastosowanie takich obliczeń jest niezbędne w kontekście przestrzegania norm budowlanych oraz standardów projektowych, które wymagają precyzyjnego określenia lokalizacji elementów budowli, aby zapewnić ich stabilność oraz bezpieczeństwo użytkowania.
Wyniki podane w odpowiedziach, które nie są zgodne z poprawną odpowiedzią, mogą wynikać z różnych błędów w interpretacji danych z rysunku oraz w obliczeniach. Na przykład, niektóre odpowiedzi mogłyby być wynikiem nieprawidłowego dodawania długości odcinków do współrzędnych punktu A. Kluczowe jest zrozumienie, że współrzędne naroża B są ściśle uzależnione od dokładnych wartości długości odcinków AB i AD, które zostały podane w zadaniu. Często pojawia się błąd, polegający na zmyleniu jednostek miar, co może prowadzić do przykładowo zaniżonego wyniku na osi X lub Y. Może to również wynikać z przesunięcia w interpretacji rysunku, co prowadzi do błędnych założeń o położeniu punktu A lub długości odcinków. Ważne jest, aby przy takich zadaniach dokładnie zrozumieć, jak długości odcinków przekładają się na zmiany w współrzędnych oraz jak geometria wpływa na końcowy wynik. Należy zwrócić uwagę na normy oraz dobre praktyki w projektowaniu i obliczeniach inżynieryjnych, które podkreślają znaczenie precyzji oraz dokładności w obliczeniach. Właściwe przeliczenia i zweryfikowanie danych są kluczowe dla uniknięcia błędów, które mogą wpływać na cały projekt budowalny oraz jego późniejsze użytkowanie.