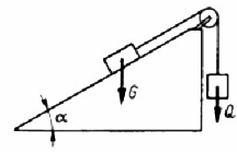
Poprawna odpowiedź to 2Q, co oznacza, że masa G powinna być dwa razy większa od masy Q, aby układ pozostał w równowadze. Wynika to z analizy równowagi sił działających na obie masy. Przy kącie nachylenia α=30°, siła ciężkości działająca na masę G na równi pochylonej można wyrazić jako G*sin(α). Dla α=30°, wartość sin(30°) wynosi 1/2, co prowadzi nas do równania G*sin(30°) = G/2. Zgodnie z równowagą sił, siła ta musi być równa sile ciężkości masy Q, która wynosi Q*g. W związku z tym, aby te siły były równe, G/2 = Q*g, co w dalszej kolejności prowadzi do wniosku, że G musi być równe 2Q. Tego rodzaju zagadnienia są kluczowe w inżynierii oraz fizyce, gdzie zrozumienie równowagi sił jest niezbędne przy projektowaniu różnorodnych konstrukcji. W praktyce, takie zasady mogą być stosowane w analizie systemów mechanicznych, co pozwala inżynierom na odpowiednie dobieranie materiałów oraz wymogów konstrukcyjnych, by zapewnić stabilność i bezpieczeństwo budowli.
Wybór niewłaściwej opcji, na przykład 3Q, 6Q lub 4Q, wskazuje na nieporozumienie dotyczące równowagi sił w kontekście równi pochylonej. W przypadku, gdy masa G ma być większa niż 2Q, siła działająca na nią na równi pochylonej staje się zbyt duża w stosunku do siły ciężkości masy Q. Przy kącie α=30°, siła działająca na masę G wynosi G*sin(30°), co prowadzi do wartości G/2. Zatem, jeśli przyjmiemy, że G=3Q, to G*sin(30°) wyniesie 3Q/2, co nie może być równoważne Q*g, bo 3Q/2 jest większe od Q. Podobnie, dla G=6Q lub G=4Q, obliczenia również prowadzą do nadmiernych sił działających na masę Q, co skutkuje brakiem równowagi. Typowym błędem myślowym w takich zadaniach jest przyjęcie, że większa masa G zawsze zwiększa stabilność układu, podczas gdy kluczowym czynnikiem jest odpowiednie zbalansowanie sił. Zrozumienie tego zagadnienia jest niezwykle ważne w praktycznych zastosowaniach inżynieryjnych, gdzie konieczne jest zachowanie równowagi w ruchach obiektów, co przekłada się na bezpieczeństwo konstrukcji oraz efektywność mechanizmów.