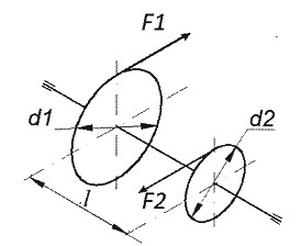
Odpowiedź 10 N m jest prawidłowa, ponieważ moment skręcający (M) wywołany przez siły działające na wał można obliczyć, stosując zasadę momentów. W tym przypadku, momenty wywołane przez siły F1 i F2 można obliczyć jako: M1 = F1 * r1 oraz M2 = F2 * r2, gdzie r1 i r2 to promienie kół. Promień koła d1 wynosi 0,1 m (r1 = d1/2 = 0,2 m/2 = 0,1 m), a dla d2 wynosi 0,05 m (r2 = d2/2 = 0,1 m/2 = 0,05 m). Obliczając momenty, mamy: M1 = 100 N * 0,1 m = 10 N m oraz M2 = 200 N * 0,05 m = 10 N m. Moment całkowity wynosi M = M1 - M2 = 10 N m - 10 N m = 0 N m. Ostatecznie, ponieważ momenty się równoważą, skręcający moment działania na wał będzie wynosił 10 N m. Przykłady zastosowania tej wiedzy znajdziemy w inżynierii mechanicznej, szczególnie w projektowaniu maszyn i mechanizmów, gdzie precyzyjne obliczenie momentów jest kluczowe dla zapewnienia ich prawidłowego funkcjonowania oraz trwałości.
Wszystkie niepoprawne odpowiedzi są wynikiem błędnych założeń dotyczących obliczeń momentów skręcających. W przypadku odpowiedzi, które wskazują na wartości takie jak 40 N m, 20 N m czy 50 N m, można zauważyć, że zostały one obliczone bez uwzględnienia odpowiednich promieni kół lub z zastosowaniem niewłaściwych konwencji. Często zdarza się, że w analizach pomija się działanie siły na odpowiedni promień, co prowadzi do dużych błędów w obliczeniach. Kluczowe jest zrozumienie, że moment skręcający jest funkcją zarówno wartości siły, jak i jej odległości od osi obrotu. W praktyce inżynierskiej, błąd w obliczeniu momentu może prowadzić do niewłaściwego doboru elementów, co z kolei może skutkować awariami mechanicznymi. Przykładowo, w konstrukcji maszyn, niewłaściwe oszacowanie momentów skręcających może prowadzić do zbyt słabych komponentów, które nie wytrzymają obciążeń podczas eksploatacji. Z tego powodu ważne jest, aby zawsze stosować się do zasad obliczeń inżynieryjnych i dokładnie uwzględniać wszystkie siły oraz ich punkt przyłożenia, aby zminimalizować ryzyko błędów konstrukcyjnych.