Kwalifikacja: PGF.07 - Wykonywanie przekazu reklamowego
Zawód: Technik reklamy
Agencja reklamowa opracowała dla klienta cennik banerów reklamowych. Oblicz brakującą cenę brutto.
Odpowiedzi
Informacja zwrotna
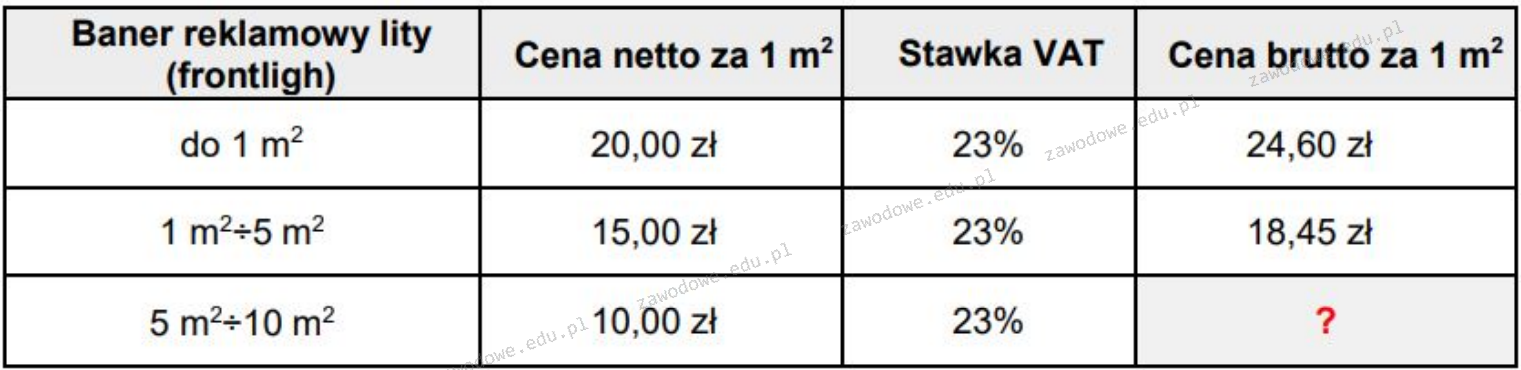
Cena brutto to cena netto powiększona o podatek VAT. W tym przypadku cena netto wynosi 10,00 zł za 1 m², a stawka VAT to 23%. Aby obliczyć cenę brutto, należy pomnożyć cenę netto przez 1,23 (czyli dodać 23% do ceny netto). Obliczenie wygląda następująco: 10,00 zł * 1,23 = 12,30 zł. Tak więc cena brutto za 1 m² wynosi 12,30 zł. To podejście jest standardem w branży, zapewniającym przejrzystość i zgodność z przepisami podatkowymi. W praktyce, wiedza ta przydaje się każdemu, kto zajmuje się sprzedażą czy zakupem towarów i usług, gdyż pozwala na prawidłowe kalkulacje cenowe i unikanie niespodzianek związanych z kwestiami podatkowymi. Dobrze jest zawsze pamiętać, że VAT jest podatkiem dodawanym do ceny netto, a jego wysokość jest określana przepisami prawa, co jest szczególnie istotne dla przedsiębiorców rozliczających się z urzędem skarbowym.
Często popełnianym błędem przy obliczaniu cen brutto jest niedokładne zrozumienie, czym jest podatek VAT i jak należy go stosować. VAT, czyli podatek od wartości dodanej, jest naliczany procentowo od ceny netto. W tym przypadku stawka wynosi 23%, co oznacza, że do ceny netto dodaje się 23% tej ceny, aby uzyskać cenę brutto. Jeśli wybiera się inne wartości niż 12,30 zł, może to wynikać z niewłaściwego zrozumienia tego mechanizmu. Częstym błędem jest np. błędne dodawanie procentów czy stosowanie niewłaściwego przelicznika. Warto też pamiętać, że kalkulacja netto-brutto jest powszechnie stosowana w większości transakcji handlowych i jest regulowana przez przepisy prawa podatkowego. W praktyce umiejętność prawidłowego obliczania VAT jest kluczowa dla każdego przedsiębiorcy, gdyż wpływa na cenę końcową oferowanych towarów czy usług, a tym samym na konkurencyjność na rynku. Ostatecznie niepoprawne kalkulacje mogą prowadzić do poważnych błędów finansowych i problemów z urzędem skarbowym. Dlatego tak ważne jest, aby zawsze dokładnie sprawdzać obliczenia i zrozumieć ich podstawy.