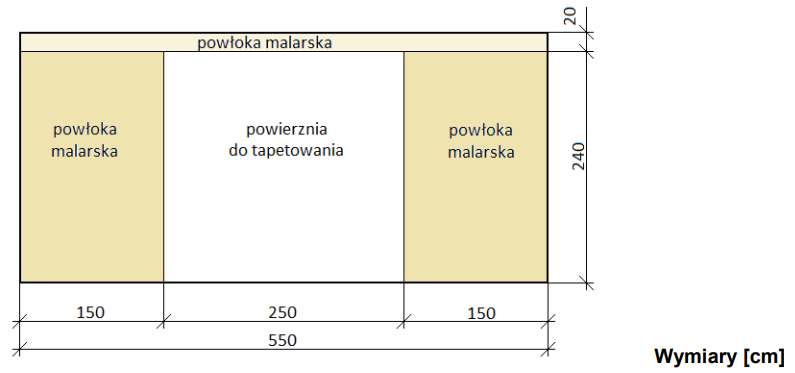
Poprawna odpowiedź wynosi 6,0 m2, co można obliczyć poprzez pomnożenie wymiarów ściany, które wynoszą 250 cm szerokości i 240 cm wysokości. Po przeliczeniu tych wartości na metry, otrzymujemy 2,5 m i 2,4 m. Obliczenie powierzchni ściany, która ma być pokryta tapetą, polega na zastosowaniu podstawowego wzoru geometrycznego: powierzchnia = szerokość × wysokość. W praktyce, znajomość tych obliczeń jest kluczowa nie tylko przy tapetowaniu, ale także w innych dziedzinach budownictwa, gdzie precyzyjne obliczenia powierzchni są niezbędne, na przykład przy malowaniu, układaniu płytek czy wykonywaniu tynków. Warto również pamiętać, aby uwzględnić ewentualne okna i drzwi, które mogą wpływać na całkowitą powierzchnię do pokrycia, co jest zgodne z dobrymi praktykami w zakresie planowania prac remontowych. Z tego względu, umiejętność dokładnego obliczania powierzchni jest istotna dla każdego, kto zajmuje się pracami wykończeniowymi.
W przypadku błędnych odpowiedzi warto zwrócić uwagę na typowe pomyłki, które mogą prowadzić do nieprawidłowych wyników. Często zdarza się, że osoby obliczające powierzchnię ściany nie przekształcają poprawnie jednostek z centymetrów na metry, co prowadzi do obliczeń w niewłaściwej skali. Przykładowo, wybierając odpowiedź 6,5 m2, można przyjąć, że błędnie obliczono szerokość lub wysokość ściany, być może dodając dodatkową wartość lub nie uwzględniając odpowiedniego przeliczenia jednostek. Dodatkowo, przy wyborze 5,5 m2, możliwe, że obliczenia też były oparte na niepoprawnych założeniach dotyczących wymiarów. Jest to typowy błąd myślowy, gdzie zamiast dokładnych pomiarów, przyjmuje się szacunkowe wartości, co w praktyce może prowadzić do znacznych różnic. Aby uniknąć takich problemów, kluczowe jest zrozumienie, że każda zmiana jednostek obliczeniowych wpływa na końcowy wynik. Dlatego zawsze upewnij się, że wymiary są przeliczone na jedną, spójną jednostkę przed dokonaniem działań matematycznych. W kontekście tapetowania, zrozumienie tych podstawowych zasad jest niezbędne, aby dokładnie oszacować ilość materiału potrzebnego do wykonania pracy oraz zminimalizować straty wynikające z błędnych obliczeń.