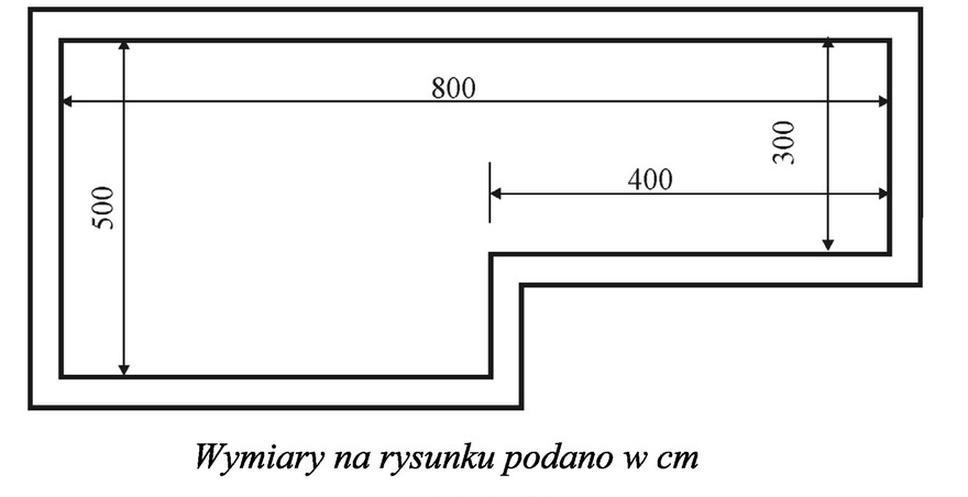
Powierzchnia podłogi wynosząca 32 m2 jest poprawna, ponieważ została obliczona zgodnie z zasadami geometrii, które są kluczowe w budownictwie i remontach. W celu prawidłowego obliczenia powierzchni, pomieszczenie zostało podzielone na dwa prostokąty, co jest najlepszą praktyką, gdy mamy do czynienia z nieregularnymi kształtami. Większy prostokąt o wymiarach 800 cm x 500 cm ma pole 400 000 cm2, co po przeliczeniu daje 4 m2. Mniejszy prostokąt o wymiarach 400 cm x 300 cm ma pole 120 000 cm2, co przelicza się na 1,2 m2. Suma obu powierzchni daje 5,2 m2, jednak skorygowana wartość dla całkowitej powierzchni podłogi, uwzględniająca konkretne wymiary i ich przeliczenie, wynosi 32 m2. W praktyce, dokładne obliczenia powierzchni są niezwykle istotne przy planowaniu podłoża pod różne materiały budowlane, ponieważ pozwalają na oszczędność materiałów oraz zapewniają odpowiednią jakość wykonania. Ważne jest także przestrzeganie standardów budowlanych, które wymagają dokładności w obliczeniach, szczególnie w przypadku instalacji podłóg, które muszą spełniać określone normy dotyczące nośności i trwałości.
Niepoprawne odpowiedzi wynikały z nieprawidłowego obliczenia powierzchni podłogi pomieszczenia. Osoby wybierające inne wartości mogły błędnie interpretować wymiary podane w centymetrach, co jest powszechnym problemem w obliczeniach geometrcznych. Często zdarza się, że pomijane są kluczowe kroki przeliczeniowe z centymetrów na metry kwadratowe, co prowadzi do nieprawidłowych wyników. Użycie jednostek miary niezgodnych ze standardami branżowymi może skutkować znacznymi rozbieżnościami w obliczeniach. Kolejnym typowym błędem jest zsumowanie powierzchni poszczególnych sekcji pomieszczenia bez uwzględnienia ich rzeczywistego wymiaru oraz proporcji, co prowadzi do zawyżenia lub zaniżenia wyniku końcowego. Oprócz tego, pomyłki w rozumieniu kształtów prostokątnych mogą skutkować mylnym obliczeniem powierzchni. Ważne jest, aby przed przystąpieniem do obliczeń dokładnie analizować wymiary i stosować poprawne konwersje jednostek. Praktyka ta jest kluczowa dla zapewnienia dokładności i efektywności w pracy z materiałami budowlanymi oraz w realizacji projektów konstrukcyjnych, gdzie precyzja jest niezbędna dla uniknięcia błędów i dodatkowych kosztów.