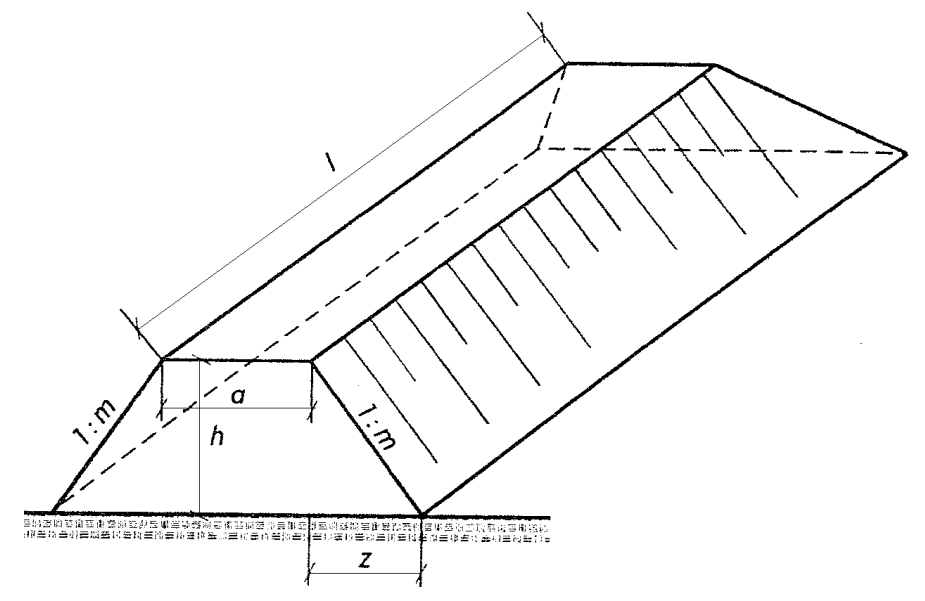
Poprawna odpowiedź wynosi 3600 m3, co można obliczyć poprzez dokładne zrozumienie geometracji nasypu. W pierwszym kroku obliczamy szerokość górnej podstawy, stosując wzór: szerokość górna = a + 2z. Dla danych a = 7 m oraz z = 2 m, uzyskujemy szerokość górną równą 11 m. Następnie, aby wyznaczyć pole przekroju poprzecznego, wykorzystujemy wzór na pole trapezu: pole = (a + szerokość górna) * h / 2. W naszym przypadku pole wynosi 18 m2, co uzyskujemy dzięki podstawieniu danych do wzoru. Wreszcie, aby obliczyć objętość nasypu, pomnożymy pole przekroju przez długość nasypu: objętość = pole * l. Dla długości l = 200 m obliczamy objętość jako 18 m2 * 200 m, co daje 3600 m3. Zrozumienie tych kroków jest kluczowe w inżynierii lądowej i budowlanej, gdzie takie obliczenia są niezbędne do projektowania i realizacji struktur inżynieryjnych. Przykłady zastosowania tej wiedzy obejmują projektowanie nasypów drogowych czy wykopów, co jest istotne w planowaniu przestrzennym oraz zarządzaniu infrastrukturą.
Wybór błędnej odpowiedzi może wynikać z kilku powszechnych błędów związanych z obliczeniami objętości nasypów. Często mylone są jednostki miary, co prowadzi do nieporozumień. Na przykład, odpowiedzi takie jak 1800 m2 czy 3600 m2 wskazują na obliczenia dotyczące pola, a nie objętości. W kontekście tego pytania, kluczowe jest zrozumienie, że do obliczenia objętości konieczne jest pomnożenie pola przekroju poprzecznego przez długość nasypu. Parkując uwagę na niepoprawnych wartościach, można zauważyć, że wynik 1800 m3 również nie odzwierciedla poprawnych obliczeń. Żeby uzyskać właściwą objętość, należy dokładnie przyjrzeć się wzorom i podstawowym zasadom geometrii, a także zastosować je w praktyce. Dodatkowo, warto pamiętać, że w inżynierii lądowej błędne zrozumienie kształtu nasypu oraz jego parametrów geometrycznych może prowadzić do drastycznych błędów w projektowaniu. Przykład niewłaściwego obliczenia objętości nasypu może skutkować nieodpowiednim doborem materiałów budowlanych, co w konsekwencji wpłynie na jakość i trwałość konstrukcji. Dlatego kluczowe jest, aby podchodząc do takich zadań, dokładnie stosować wzory i upewnić się, że rozumiemy każdy element problemu, aby uniknąć nieporozumień oraz błędów w obliczeniach.