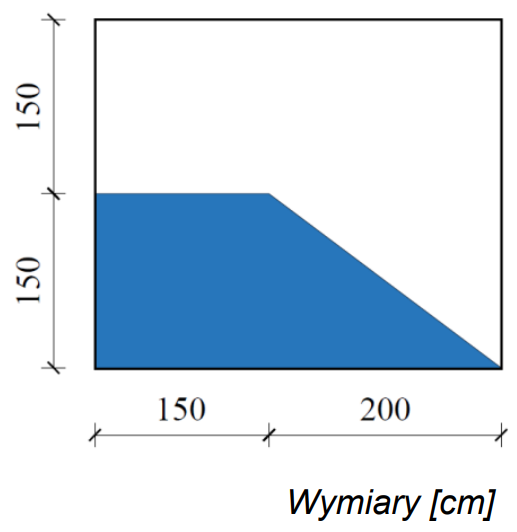
Powierzchnia zaznaczonego fragmentu ściany wynosząca 3,75 m2 została obliczona na podstawie precyzyjnych działań matematycznych, które uwzględniają geometrę zarówno trapezu, jak i prostokąta. Obliczenia te są zgodne z zasadami geometrii, gdzie powierzchnię trapezu można wyliczyć ze wzoru: (a + b) * h / 2, gdzie a i b to długości podstaw, a h to wysokość trapezu. W przypadku prostokąta, obliczamy powierzchnię jako długość razy szerokość. Tego rodzaju obliczenia znajdują zastosowanie w wielu dziedzinach, w tym budownictwie i projektowaniu wnętrz, gdzie dokładność pomiarów ma kluczowe znaczenie. Stosowanie odpowiednich narzędzi pomiarowych oraz przestrzeganie standardów branżowych, takich jak ISO 9001, zapewnia wysoką jakość i precyzję zrealizowanych prac. Warto również zaznaczyć, że umiejętność poprawnego obliczania powierzchni jest przydatna w codziennym życiu, na przykład przy zakupie farby, gdzie znajomość metody obliczeń pozwala na dokładne oszacowanie potrzebnej ilości materiałów.
Wybór niepoprawnej odpowiedzi może wynikać z kilku błędów w analizie powierzchni zaznaczonego fragmentu ściany. Często mylone są pojęcia związane z obliczaniem powierzchni różnych figur geometrycznych. Na przykład, w przypadku trapezu, kluczowe jest prawidłowe zidentyfikowanie długości podstaw i wysokości, co może prowadzić do znaczących błędów, jeżeli jeden z tych parametrów zostanie niewłaściwie oszacowany. Ponadto, w obliczeniach prostokąta, pomyłki przy pomiarze długości lub szerokości mogą również skutkować nieprawidłowym wynikiem. W praktyce, wiele osób może również nie uwzględniać dodatkowych czynników, takich jak różnice w kształcie ściany czy obecność elementów dekoracyjnych, które mogą zmieniać rzeczywistą powierzchnię do malowania. Czasami zdarza się, że niektórzy mogą mylić jednostki miary, co prowadzi do użycia niewłaściwych wartości w obliczeniach. Dlatego też, dla poprawnego obliczenia powierzchni, kluczowe jest stosowanie dobrych praktyk, takich jak dokładne pomiary, zastosowanie odpowiednich wzorów matematycznych oraz potwierdzenie obliczeń poprzez ich wielokrotne sprawdzenie. Takie podejście pozwoli uniknąć powszechnych pułapek i zapewni dokładność potrzebnych danych.