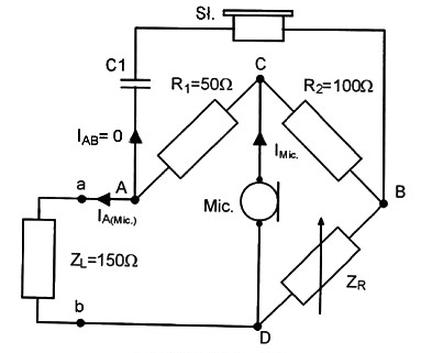
Odpowiedź 300 Ω jest prawidłowa, ponieważ w warunkach zrównoważenia mostka Wheatstone'a stosunek rezystancji w jednym ramieniu musi odpowiadać stosunkowi rezystancji w drugim ramieniu. Jeśli założymy, że w jednym ramieniu mamy rezystancję R1, a w drugim R2, to przy zrównoważonym układzie można zapisać równanie R1 / R2 = Z1 / ZR. W tym przypadku, jeśli stosunek R1 do Z1 wynosi 1/3, to aby zachować równowagę, impedancja R2 (ZR) musi być trzykrotnie większa. Oznacza to, że jeżeli R2 wynosi 100 Ω, to ZR powinno wynosić 300 Ω. Praktyczne zastosowanie tej zasady można zauważyć w pomiarach rezystancji, gdzie mostek Wheatstone'a jest wykorzystywany do precyzyjnego określania wartości nieznanych rezystancji, co jest szczególnie istotne w laboratoriach badawczych i przemyśle elektronicznym. Właściwe zrozumienie zasad zrównoważenia mostka jest kluczowe dla inżynierów zajmujących się projektowaniem układów elektronicznych, zapewniając dokładność i precyzję w obliczeniach.
W przypadku wyboru odpowiedzi 600 Ω, 800 Ω lub 1200 Ω, kluczowym błędem jest niezrozumienie zasady zrównoważenia mostka Wheatstone'a. W mostku tym, aby uzyskać równowagę, należy przestrzegać zasady, że stosunek rezystancji w dwóch ramionach musi pozostać równy. Wybierając 600 Ω, można pomyśleć, że jest to wartość, która odpowiada zrównoważeniu, jednak nie uwzględnia ona proporcji zachodzącej między rezystancjami. Jeśli R1 jest 100 Ω i Z1 jest 300 Ω, to stosunek R1 do Z1 wynosi 1:3, co nie jest spełnione dla 600 Ω. Przy wyborze 800 Ω lub 1200 Ω obserwujemy dalej naruszenie zasady proporcjonalności, ponieważ ZR musi być dokładnie trzykrotnością R2, a nie inną wartością. Typowe błędy myślowe obejmują również zakładanie, że jakakolwiek wartość wyższa niż 300 Ω będzie poprawna, co jest nieprawidłowe, ponieważ nie odnosi się do rzeczywistych obliczeń opartych na pomiarach i zasadzie zrównoważenia. W praktyce, zrozumienie tych zasad jest niezbędne przy projektowaniu układów pomiarowych i zapewnieniu zgodności z normami metrologicznymi.